class: left, top, inverse, title-slide .title[ # <strong>Metapopulations: Part I</strong> ] .subtitle[ ## <a href="https://eligurarie.github.io/EFB370/">EFB 370: Population Ecology</a> ] .author[ ### .white[**Dr. Elie Gurarie]** ] .date[ ### .white[March 18, 2024] ] --- <style type="text/css"> MathJax.Hub.Config({ tex2jax: { inlineMath: [['$','$'], ['\\(','\\)']], processEscapes: true } }); </style> <!-- ## Goals .pull-left[ ] .pull-right[Gotelli Chapter 4] --> # Some important announcements .pull-left-60.large[ 1. Age structure homework (Tasmanian Devils) dues **Thursday**. 2. Next Monday is **Exam 2** on March 25th. 3. Last year's exam is in the **Week 9** Blackboard Folder. I will review this exam during the recitation period this week (in **Baker 145**). 4. **Colton** will be having extra office ours in addition to MTW 12-12:45: in *Illick 407* Thursday 12-2 and Friday 12-2. ] --- # Goals: .pull-left-30[ Define ***metapopulation*** How does **metapopulation structure** influence **extinction probabilities** Some theoretical models: - **External** and **Internal** colonization - **Independent mortality** vs. **Rescue Effect** ] .pull-right-70.center[] --- ## Blowing up `\(N_t\)` in space **Simple population:** `$$\large N(t)$$` **Age/stage-structured:** `$$\large N_i(t) = \{N_1(t), N_2(t), ..., N_k(t)\}$$` - where `\(i\)` represents structure, with `\(k\)` age/stage classes **Spatial structure:** `$$\large N_i(t) = \{N_1(t), N_2(t), ..., N_k(t)\}$$` - where `\(i\)` is location, with `\(k\)` locations --- ## .darkblue[A metapopulation is a **population of populations**] .pull-left[ 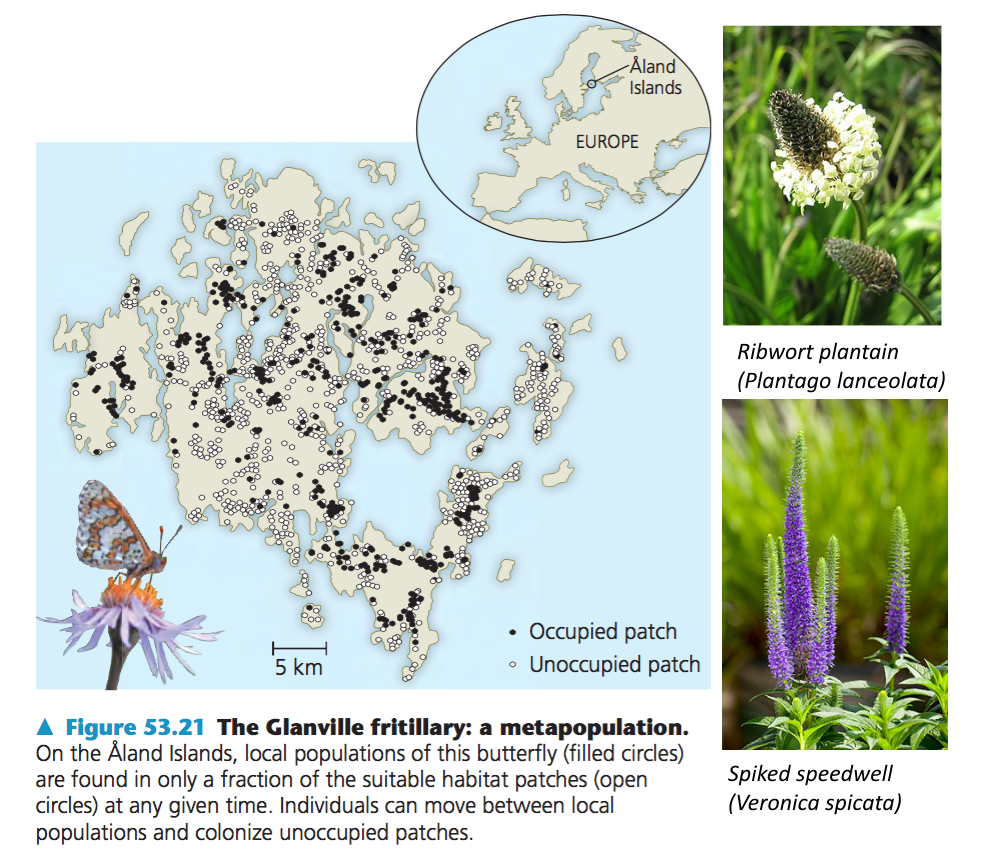] .pull-right.large[ 1. The local populations MUST be somehow connected via **dispersal**. 2. There must be areas of (near) zero density in between. The "in-between" is referred to as the **matrix**. ### Canonical examples - **Fragmented habitats** - Island populations ] --- ## **Population** vs. **Metapopulation** .pull-left-40.large[ **WA sea otters** - Closed population - only **Birth** and **Death** - Questions: - growth | dynamics | age structures - **Extinction** of interest mainly due to stochasticity, low numbers ] .pull-right-50.large[ **ALL sea otters** - Open population - **Immigration!** **Emigration!** - Questions: - given that a local population might go **extinct**, will the metapopulation go **extinct**? - what is the proportion of occupied patches? ] --- ## What makes it a metapopulation? **Dispersal distance** .pull-left[ 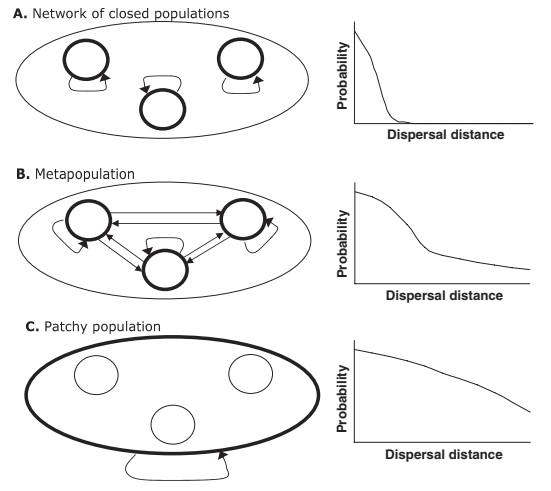 Sale, Hanski, Kritzer 2006 ] .pull-right.large[ As long as there is *some* local connectivity among populations. 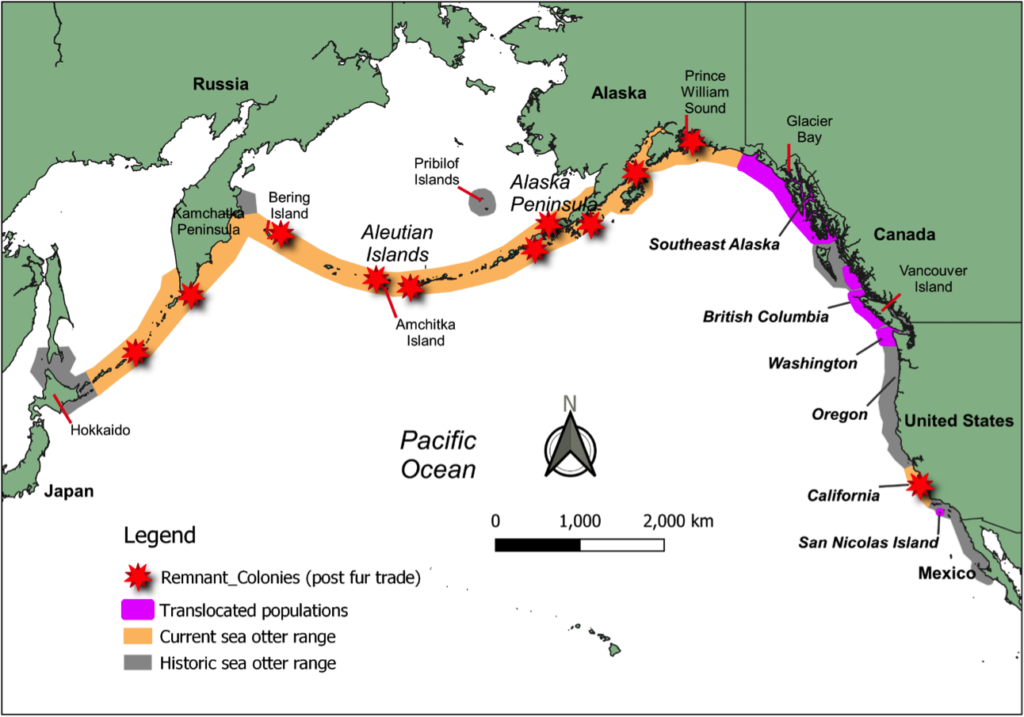 ] --- .pull-left-60[ ## By that metric ... ### Polar bear (*Ursus maritimus*) 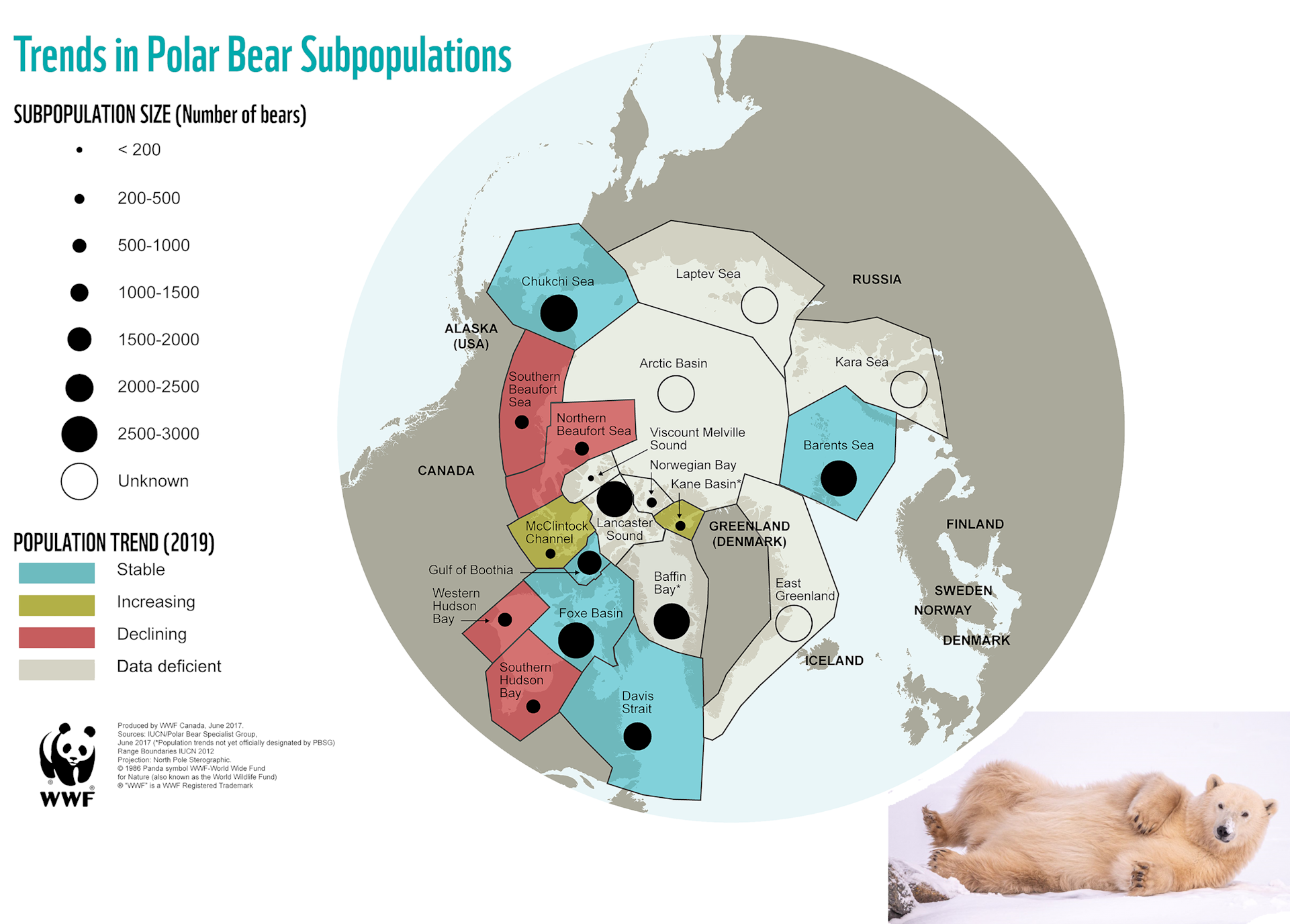 ] .pull-right-40[ ### and caribou / reindeer (*Rangifer tarandus*)  .center[Are also **metapopulations**] ] --- .pull-left.large[ ## **How long does a population persist?** 1. **YOU** are a small population with some risk of extinction 2. Take a die 3. Stand at your spot. Wait for the year command. 3. Roll the die once. 4. If it is a ⚅ - you went extinct. 5. If you are not extinct, repeat. Otherwise, enter data in form at right. ] .pull-right[] --- ## Population persistence of a single population? .pull-left[ `\(e\)` = *local* probability of extinction time steps | Prob. persistence ---|--- 1: | `\(1-e\)` 2: | `\((1-e)(1-e)\)` 3: | `\((1-e)(1-e)(1-e)\)` 4: | `\((1-e)(1-e)(1-e)(1-e)\)` ... | `\(t\)`: | `\((1-e)^t\)` ] .pull-right[ <img src="Metapopulations_PartI_files/figure-html/localpersistence-1.png" width="100%" /> **Take away:** Even with very LOW probability of extinction, you WILL go extinct. ] --- ## **M0**: Population persistence of a **metapopulation** .pull-left-40[ `\(k\)` populations, `\(t\)` time steps Pops: | 1 time step| *t* steps ---|---|---- 1: | `\(1-e\)` | `\((1-e)^t\)` 2: | `\(1-e \times e\)` | `\((1-e^2)^t\)` 3: | `\(1-e \times e \times e\)` | `\((1-e^3)^t\)` ... | ... | ... k: | `\(1-e^k\)` | `\((1-e^k)^t\)` ] .pull-right-60[ <img src="Metapopulations_PartI_files/figure-html/unnamed-chunk-3-1.png" width="100%" /> ] --- ## Metapopulations are resistant to extinction! .pull-left-40[ `$$\large P(k,t) = (1-e^k)^t$$` .darkblue[ Metapopulations **dramatically** spread out / buffer the risk of extinction!] <center> <img src='images/tornado.jpg' width='50%'/> </center> .darkred[ But still ... if the ONLY process is extinction, you **will go extinct** (sorry!) ] ] .pull-right-60[ <img src="Metapopulations_PartI_files/figure-html/unnamed-chunk-4-1.png" width="100%" /> ] --- ## **M1:** Let's add **colonization** .pull-left.large[ **Island-Mainland model** - Every (local) population has a probability of going extinct: `\(\Large p_e\)` - But every empty location has a probability of getting colonized: `\(\Large p_c\)` > Note - there is an important (implicit) assumption that population very quickly hits **carrying capacity**, so essentially *instant* saturation. ] .pull-right.large[ 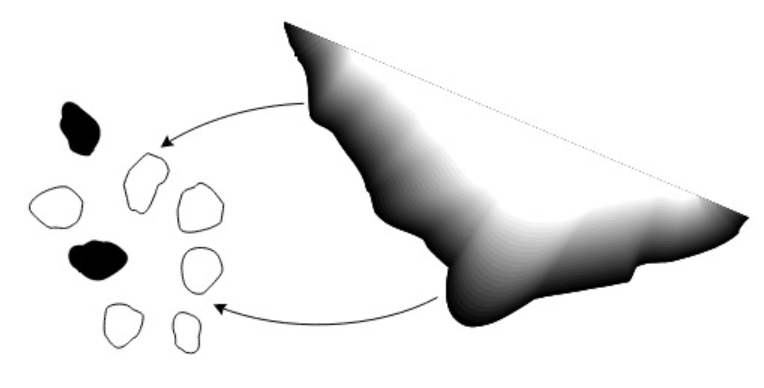 The mainland is a constant, independent source of potential colonizers. Also known as **propagule rain**. .green[(echoes of *biogeography*).] ] --- ## **M1:** Let's add **colonization** .pull-left.large[ .box-blue[ 1. **YOU** are a small unoccupied patch. 3. If you are unoccupied, roll a die. If it is **even** you've been colonized. Stand up. 2. If you are occupied, roll a die. If it's a ⚅ - you went extinct. 4. Let's count! ... and back to the top. ] ] .pull-right.large[  ] --- ## **M1:** Island-Mainland Model .pull-left[ ### Q: How many occupied patches might we expect? `$$E(N_{t+1}) = N_t - p_e N_t + (K - N_t)\,p_c$$` define proportion of populated patches: `\(f_t = E(N_t)/K\)`, and define *equilibirum*: `$$f^* := f_{t+1} = f_t$$` .center[*...then some math happens...*] .red[$$\large f^* = {p_c \over p_c + p_e}$$] ] .pull-right[  > The equilibrium is a balance between colonization and extinction rate. ] --- ## Continuous time formulation .pull-left-40[ Very general metapopulation model: .red[ `$$\huge {df \over dt} = c(f) - e(f)$$` ] Where *c* = colonization rate, *e* = extinction rate. Can be (often are!) functions of `\(f\)` (occupied proportion). .green[Note: this is similar to `$$\large {dN \over dt} = b(N) - d(N).$$` which is the foundation of population growth models) ]] .pull-right-50[ > #### Assumptions: > > - Deterministic (i.e. `\(k \to \infty\)`) > - Continuous-time, unstructured extinction / colonization process > - "Rates" are like infinitesemal probabilities But - lots of elegant analyses can be made messing with this model. ] --- .pull-left[ ## **M1:** Mainland-Island .large.red[ `$$\large {df \over dt} = c - e$$` ] Colonization is constant, so proportional to **available** patches: `$$\Large c = p_c(1-f)$$` Extinction is constant, so proportional to **occupied** patches: `$$\Large e = p_e f$$` so: $$ {df \over dt} = p_c(1-f) - p_ef$$ ] .pull-right[ <img src="Metapopulations_PartI_files/figure-html/IslandMainland-1.png" width="100%" /> > The rate of change of the occupied patches GROWS in proportion to unoccupied patches and FALLS in proportion with occupied patches. ] --- ## **M2**: Internal Colonization .red[$$\Large {df \over dt} = p_c f(1-f) - p_ef$$] .pull-left-30[ 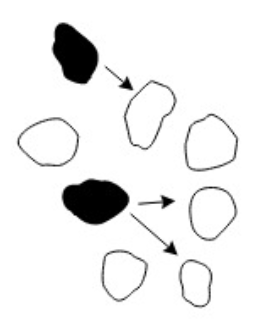 ] .pull-right-60.large[ Extinction *rate* is constant, as before: `$$e = p_e f$$` Colonization can only come from **occupied** patches: `$$c = p_c \, f \, (1-f)$$` If no patch is colonized ( `\(f=0\)` ), nothing can colonize. If the population is 100% occupied ( `\(f = 1\)` ), there is nothing to colonize. ] --- .pull-left-30[   ] .pull-right-70.large[ ## **M2**: Internal Colonization ### Human Experiment I .box-blue[ 1. **YOU** are a small unoccupied patch. 2. If you are occupied, roll a die: - If it's a ⚀ - you went extinct. - If it's a ⚄ or a ⚅ - you "colonize" a neighboring patch. 3. Let's count! ... and back to the top. ] #### What do to you think the equilibrium _f_^*will be? ] --- .pull-left-30[   ] .pull-right-70.large[ ## **M2**: Internal Colonization ### Human Experiment I .box-blue[ 1. **YOU** are a small unoccupied patch. 2. If you are occupied, roll a die: - If it's a ⚄ or a ⚅ - you went extinct. - If it's a ⚀ - you "colonize" a neighboring patch. 3. Let's count! ... and back to the top. ] #### Now what do to you think the equilibrium _f_^*will be? ] --- .pull-left[ ## **M2**: Internal Colonization - with Schematic .red[ $$ \large {df \over dt} = p_c f(1-f) - p_ef$$ ] Extinction is constant, as before: `$$e = p_e f$$` Colonization can only come from **occupied** patches: `$$c = p_c \, f \, (1-f)$$` .blue[The maximum rate of colonization occurs when `\(f = 1/2\)`. ] ] .pull-right[ <img src="Metapopulations_PartI_files/figure-html/InternalColonization-1.png" width="100%" /> **Equilibrium** occurs when: .darkred[ `$$f^* = \begin{cases} 1-p_e/p_c & \text{when} & p_e < p_c \\ 0 & \text{when} & p_e \geq p_c\end{cases}$$` ]] --- ## **M3:** Rescue Effect .red[ $$ \Large {df \over dt} = p_c (1-f) - p_ef(1-f)$$ ] .pull-left-40[ Assumes that if you have a lot of neighbors some loose "propagules" will buffer you from extinction. **Equilibrium states:** .darkred[ `$$f^* = \begin{cases} p_c/p_e & \text{when} & p_e > p_c \\ 1 & \text{when} & p_e \leq p_c\end{cases}$$` ] Even with higher extinction rate than colonization rate, there will always be some occupied patches! ] .pull-right[ <img src="Metapopulations_PartI_files/figure-html/RescueEffect-1.png" width="100%" /> ] --- ## **M4:** Rescue Effect with Internal Colonization <font color = "red"> $$ \large {df \over dt} = p_c f(1-f) - p_ef(1-f)$$ </font> .pull-left[ Only equilibria: 0, if `\(p_e > p_c\)` or 1, if `\(p_e \leq p_c\)`. Fundamental conclusions: > **metapopulation** under equilibrium MUST be rare! > Either everything colonizes or nothing colonizes. ] .pull-right[ <img src="Metapopulations_PartI_files/figure-html/FinalSchematic-1.png" width="100%" /> ] --- ## Four models <center> <img src="Metapopulations_PartI_files/figure-html/unnamed-chunk-5-1.png" width="70%" /> With rather different predictions! (Nice synthesis - mainly due to Gotelli.) --- .pull-left-70[ ## Some characters ### Richard Levins (1930-2016)  - "Scholarship that is indifferent to human suffering is immoral." - "Our truth is the intersection of independent lies." ] .pull-right-30[ ### Ilkka Hanski (1953-2016)  ]