class: center, middle, white, title-slide .title[ # How to model just about anything<br>(but especially habitat) ] .subtitle[ ## EFB 390: Wildlife Ecology and Management ] .author[ ### Dr. Elie Gurarie ] .date[ ### September 28, 2023 ] --- <!-- https://bookdown.org/yihui/rmarkdown/xaringan-format.html --> ## Super fast primer on statistical modeling Everything you need to know to do 95% of all wildlife modeling in less than an hour and **FOUR** (or **FIVE**) easy steps!! .pull-left.large[ **I.** Linear modeling **II.** Multivariate modeling **III.** Model selection ] .pull-right.large[ **IV.** Generalized linear modeling - Poisson; Binomial **V.** Prediction ] --- .pull-left-70[ # **Step I:** Linear modeling ... is a very general method to quantifying relationships among variables. .pull-left[ <!-- --> ] .pull-right[ `\(X_i\)` - is called: - covariate - independent variable - explanatory variable `\(Y_i\)` - is the property we are interested in modeling: - response variable - dependent variable .small[Note: There actually can be interest in wildlife studies to have models for **length** and **weight**, since **length** is easy to measure (e.g. from drones), but **weight** tells us more about physical condition and energetics.] ] ] .pull-right-30[  Steller sea lion (*Eumatopias jubatus*) pups. ] --- # Linear Models .pull-left[ #### Deterministic: `$$Y_i = a + bX_i$$` `\(a\)` - intercept; `\(b\)` - slope ] .pull-right[ #### Probabilistic: `$$Y_i = \alpha + \beta X_i + \epsilon_i$$` `\(\alpha\)` - intercept; `\(\beta\)` - slope; `\(\epsilon\)` - **randomness!**: `\(\epsilon_i \sim {\cal N}(0, \sigma)\)` ] .pull-left[ <!-- --> ] .pull-right[ <!-- --> ] --- # Fitting linear models is very easy in ! .pull-left[ **Point Estimate** This command fits a model: .small[ ```r lm(Weight ~ Length, data = pups) ``` ``` ## ## Call: ## lm(formula = Weight ~ Length, data = pups) ## ## Coefficients: ## (Intercept) Length ## -49.1422 0.7535 ``` ] So for **each 1 cm** of length, add another **754 grams**, i.e. `\(\widehat{\beta} = 0.754\)` ] .pull-right[ ```r plot(Weight ~ Length, data = pups) abline(my_model) ``` <!-- --> The `abline` puts a line, with intercept `a` and slope `b` onto a figure. ] --- .pull-left-60[ # Statistical inference **Statistical inference** is the *science / art* of observings *something* from a **portion of a population** and making statements about the **entire population**. In practice - this is done by taking **data** and **estimating parameters** of a **model**. (This is also called *fitting* a model). Two related goals: 1. obtaining a **point estimate** and a **confidence interval** (precision) of the parameter estimate. 2. Assessing whether particular (combinations of) factors, i.e. **models**, provide any **explanatory power**. This is (almost always) done using **Maximum Likelihood Estimation**, i.e. an algorithm searches through possible values of the parameters that make the model **MOST LIKELY** (have the highest probability) given the data. ] .pull-right-40[  .small[Another gratuitous sea lion picture.] ] --- # All models have these pieces: `$$\Huge Y = f({\bf X} | \bf{\Theta})$$` - **Y** - response | dependent variable. The thing we want to model / predict / understand. The **effect** (maybe). - **X** - predictor(s) | independent variable(s) | covariate(s). The thing(s) that "explain(s)" **Y**. The **cause** (maybe). - **f** - the model structure. This includes: some **deterministic functional form** form (*linear? periodic? polynomial? exponential?*) AND some **probabilistic assumptions**, i.e. a way to characterize the variability / randomness / unpredictability of the process. - `\(\bf \Theta\)` - the parameters of the model. There are usually some parameters associated with the **predictors**, and some associated with the **random bit**. --- # Goals (Art / Science) of Modeling `$$\Huge Y = f({\bf X} | \bf{\Theta})$$` .pull-left[ ### 1. Model fitting .darkred[ What are the **best** `\(\bf \Theta\)` values given `\(f, {\bf X}, Y\)`? ] **Fitting the model** = **estimating the parameters**. Usually according to some criterion (almost always **Maximum Likelihood**. ] -- .pull-right[ ### 2. Model selection .darkred[ What are the **best** of a set of models `\(f_1\)`, `\(f_2\)`, `\(f_3\)` given `\(\bf X\)` and `\(Y\)`? ] Different models *usually* vary by what particular variables go into **X**, but can also vary by **functional form** and **distribution assumptions** Use some **Criterion** (e.g. AIC) to "select" the best model, which balances **how many parameters you estimated** verses **how good the fit is**. ] --- # Whoa! What is "Maximum Likelihood"!? .pull-left[ ### Oakie  ] .pull-right[ ### Orange  ] .red.center.large[**Q:** What is the "best model" for squirrel morph distribution?] --- `$$\Huge Y = f({\bf X} | \bf{\Theta})$$` .pull-left[ #### Linear model Two ways to write the same thing: `$$Y_i = \alpha + \beta X_i + \epsilon_i$$` `$$Y_i \sim {\cal N}(\alpha + \beta X_i, \sigma)$$` <!-- --> ] .pull-right.large[ - Response `\(Y\)` - Weight - Predictor `\(X\)` - Length - Parameters `\(\Theta\)`: `\(\alpha\)`; `\(\beta\)`; `\(\sigma\)` - Function `\(f()\)`: Normal distribution `\({\cal N()}\)` ] --- .pull-left-60[ ## Statistical output `$$\large Y_i \sim {\cal N}(\alpha + \beta X_i, \sigma)$$` <font size="4"><pre> ``` ## ## Call: ## lm(formula = Weight ~ Length, data = pups %>% subset(Island == ## "Raykoke")) ## ## Residuals: ## Min 1Q Median 3Q Max ## -7.498 -1.718 0.023 1.764 7.276 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -49.14222 5.75796 -8.535 1.81e-13 *** ## Length 0.75345 0.05193 14.510 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.761 on 98 degrees of freedom ## Multiple R-squared: 0.6824, Adjusted R-squared: 0.6791 ## F-statistic: 210.5 on 1 and 98 DF, p-value: < 2.2e-16 ``` </pre></font> ] -- .pull-right-40[ ### 1. Point estimates and confidence intervals .red.center[ **Intercept** ( `\(\alpha\)` ): `\(-49.14 \pm 11.5\)` **Slope** ( `\(\beta\)` ): `\(0.75 \pm 0.104\)` ] ### 2. Is the model a good one? *p*-values are very very small, in particular for **slope** Proportion of variance explained is high: .blue.large[$$R^2 = 0.68$$] ] --- ### Models and Hypotheses > .large[**Every *p*-value is a Hypothesis test.**] > .center[ <table class="table" style="margin-left: auto; margin-right: auto;"> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:right;"> Estimate </th> <th style="text-align:right;"> Std. Error </th> <th style="text-align:right;"> t value </th> <th style="text-align:right;"> Pr(>|t|) </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> (Intercept) </td> <td style="text-align:right;"> -49.142 </td> <td style="text-align:right;"> 5.758 </td> <td style="text-align:right;"> -8.535 </td> <td style="text-align:right;"> 0 </td> </tr> <tr> <td style="text-align:left;"> Length </td> <td style="text-align:right;"> 0.753 </td> <td style="text-align:right;"> 0.052 </td> <td style="text-align:right;"> 14.510 </td> <td style="text-align:right;"> 0 </td> </tr> </tbody> </table> ] .large[ - First hypothesis test: `\(H_0\)` .darkred[intercept = 0] - Second hypothesis: `\(H_0\)` .blue[slope = 0] Both null-hypotheses strongly rejected. ] --- ## But other variables might influence pup size .pull-left-30[ Lots of competing models with different **main** and **interaction** effects. ] .pull-right-70[ <!-- --> ] --- ## Linear modeling with a discrete factor .center[ `\(Y_{ij} = \alpha + \beta_i + \epsilon_{ij}\)` ] `\(i\)` is the index of sex (*Male* or *Female*), so there are two "Sex effects" - `\(\beta_1\)` and `\(\beta_2\)` representing the effect of the sex group; *j* is the index of the individual within each sex group *i*. .pull-left-50[ <!-- --> ] .pull-right[ ```r lm(Weight ~ Sex, data = pups) ``` .footnotesize[ <table> <thead> <tr> <th style="text-align:left;"> term </th> <th style="text-align:right;"> estimate </th> <th style="text-align:right;"> std.error </th> <th style="text-align:right;"> statistic </th> <th style="text-align:right;"> p.value </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> (Intercept) </td> <td style="text-align:right;"> 30.151 </td> <td style="text-align:right;"> 0.317 </td> <td style="text-align:right;"> 95.119 </td> <td style="text-align:right;"> <2e-16 </td> </tr> <tr> <td style="text-align:left;"> SexMale </td> <td style="text-align:right;"> 6.149 </td> <td style="text-align:right;"> 0.429 </td> <td style="text-align:right;"> 14.337 </td> <td style="text-align:right;"> <2e-16 </td> </tr> </tbody> </table> ] *Intercept* here means mean **female** weight. Note - this is very similar to a *t*-test comparing two means (baby stats). ] --- ## Linear modeling with multiple factors Very easy to extend this to more complicated models! .pull-left-50[ <!-- --> ] .pull-right[ .center.large.green[ `\(Y_{ijk} = \alpha + \beta_i \, \text{Island}_{ijk} + \gamma_j \, \text{Sex}_{ijk} + \epsilon_{ijk}\)` ] ```r lm(Weight ~ Island + Sex, data = pups) ``` .footnotesize[ <table> <thead> <tr> <th style="text-align:left;"> term </th> <th style="text-align:right;"> estimate </th> <th style="text-align:right;"> std.error </th> <th style="text-align:right;"> statistic </th> <th style="text-align:right;"> p.value </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> (Intercept) </td> <td style="text-align:right;"> 31.04 </td> <td style="text-align:right;"> 0.54 </td> <td style="text-align:right;"> 57.62 </td> <td style="text-align:right;"> <1e-16 </td> </tr> <tr> <td style="text-align:left;"> IslandChirpoev </td> <td style="text-align:right;"> -2.23 </td> <td style="text-align:right;"> 0.67 </td> <td style="text-align:right;"> -3.34 </td> <td style="text-align:right;"> 0.001 </td> </tr> <tr> <td style="text-align:left;"> IslandLovushki </td> <td style="text-align:right;"> -0.84 </td> <td style="text-align:right;"> 0.67 </td> <td style="text-align:right;"> -1.26 </td> <td style="text-align:right;"> 0.21 </td> </tr> <tr> <td style="text-align:left;"> IslandRaykoke </td> <td style="text-align:right;"> 0.14 </td> <td style="text-align:right;"> 0.67 </td> <td style="text-align:right;"> 0.21 </td> <td style="text-align:right;"> 0.83 </td> </tr> <tr> <td style="text-align:left;"> IslandSrednova </td> <td style="text-align:right;"> -1.50 </td> <td style="text-align:right;"> 0.67 </td> <td style="text-align:right;"> -2.24 </td> <td style="text-align:right;"> 0.03 </td> </tr> <tr> <td style="text-align:left;"> SexMale </td> <td style="text-align:right;"> 6.14 </td> <td style="text-align:right;"> 0.42 </td> <td style="text-align:right;"> 14.47 </td> <td style="text-align:right;"> 1e-16 </td> </tr> </tbody> </table> ] ] --- ## Analysis of Variance (ANOVA) Is a technique for seeing which effect in a model is **significant**. Each row tests a **hypothesis** that the effect coefficients are non-zero. .pull-left-60[ In this model, we include an **interaction**, asking: "*Do different Islands have different patterns among Sexes? (and vice versa)*" .center[`lm(Weight ~ Island * Sex, data = pups)`] .content-box-blue[ .small[<pre>Analysis of Variance Table Response: Weight Df Sum Sq Mean Sq F value Pr(>F) Island 4 443.3 110.8 5.0114 0.0005763 *** Sex 1 4623.9 4623.9 209.0758 < 2.2e-16 *** Island:Sex 4 71.4 17.9 0.8075 0.5207439 Residuals 488 10792.6 22.1 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 </pre>] ] .blue[**Non-significant interaction term**] ] .pull-right-40[ ### Interpretation: - Differences between SEXES very significant (.red[very very small p-value]) - Differences among ISLANDS very significant (.red[small p-value]) - SEX differences among ISLANDS consistent (.blue[large **interaction** *p*-value]) - ISLANDS differences between SEXES consistent (.blue[large **interaction** *p*-value]) ] --- ## Combining **continuous** and **categorical** variables .pull-left[ **Exploratory plot** .center[ <img src="Lecture_Modeling_files/figure-html/unnamed-chunk-22-1.png" width="90%" /> ] It looks like, maybe, there are different body proportions for .blue[**MALES**] and .red[**FEMALES**]. ] -- .pull-right[ ### **ANOVA** table confirms our suspicion! .content-box-blue[ .footnotesize[<pre>Analysis of Variance Table Response: Weight Df Sum Sq Mean Sq F value Pr(>F) Length 1 12413.8 12413.8 1957.969 < 2.2e-16 *** Sex 1 257.3 257.3 40.582 4.321e-10 *** Length:Sex 1 128.1 128.1 20.208 8.662e-06 *** Residuals 494 3132.0 6.3 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 </pre>] ] .large.darkred[Highly significant **interaction** term.] ] --- .pull-left[ # **Step III:** Model Selection ANOVA is helpful for "nested" models, where each one is a subset of another more complex one. For comparing a **set of competing,non-nested** models, we use . .footnotesize[ ### `\(\Delta\)`AIC table <table class="table" style="margin-left: auto; margin-right: auto;"> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:left;"> Model </th> <th style="text-align:right;"> k </th> <th style="text-align:right;"> R2 </th> <th style="text-align:right;"> logLik </th> <th style="text-align:right;"> AIC </th> <th style="text-align:right;"> dAIC </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> M0 </td> <td style="text-align:left;"> 1 </td> <td style="text-align:right;"> 1 </td> <td style="text-align:right;"> 0.000 </td> <td style="text-align:right;"> -1569.5 </td> <td style="text-align:right;"> 3143.1 </td> <td style="text-align:right;"> 835.8 </td> </tr> <tr> <td style="text-align:left;"> M1 </td> <td style="text-align:left;"> Island </td> <td style="text-align:right;"> 5 </td> <td style="text-align:right;"> 0.028 </td> <td style="text-align:right;"> -1562.5 </td> <td style="text-align:right;"> 3137.0 </td> <td style="text-align:right;"> 829.7 </td> </tr> <tr> <td style="text-align:left;"> M2 </td> <td style="text-align:left;"> Sex </td> <td style="text-align:right;"> 2 </td> <td style="text-align:right;"> 0.293 </td> <td style="text-align:right;"> -1483.2 </td> <td style="text-align:right;"> 2972.4 </td> <td style="text-align:right;"> 665.1 </td> </tr> <tr> <td style="text-align:left;"> M3 </td> <td style="text-align:left;"> Length </td> <td style="text-align:right;"> 2 </td> <td style="text-align:right;"> 0.779 </td> <td style="text-align:right;"> -1193.4 </td> <td style="text-align:right;"> 2392.8 </td> <td style="text-align:right;"> 85.5 </td> </tr> <tr> <td style="text-align:left;"> M4 </td> <td style="text-align:left;"> Length + Sex </td> <td style="text-align:right;"> 3 </td> <td style="text-align:right;"> 0.795 </td> <td style="text-align:right;"> -1174.5 </td> <td style="text-align:right;"> 2357.0 </td> <td style="text-align:right;"> 49.7 </td> </tr> <tr> <td style="text-align:left;"> M6 </td> <td style="text-align:left;"> Length * Sex </td> <td style="text-align:right;"> 4 </td> <td style="text-align:right;"> 0.803 </td> <td style="text-align:right;"> -1164.5 </td> <td style="text-align:right;"> 2339.0 </td> <td style="text-align:right;"> 31.7 </td> </tr> <tr> <td style="text-align:left;"> M5 </td> <td style="text-align:left;"> Length + Sex + Island </td> <td style="text-align:right;"> 7 </td> <td style="text-align:right;"> 0.811 </td> <td style="text-align:right;"> -1155.0 </td> <td style="text-align:right;"> 2325.9 </td> <td style="text-align:right;"> 18.6 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> M7 </td> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> Length * Sex + Island </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 8 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 0.818 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> -1144.6 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 2307.3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 0.0 </td> </tr> <tr> <td style="text-align:left;"> M8 </td> <td style="text-align:left;"> Length * Sex * Island </td> <td style="text-align:right;"> 20 </td> <td style="text-align:right;"> 0.824 </td> <td style="text-align:right;"> -1137.1 </td> <td style="text-align:right;"> 2316.1 </td> <td style="text-align:right;"> 8.8 </td> </tr> </tbody> </table> ] ] .pull-right[ **Degrees of freedom *k*:** - Number of estimated parameters. Measure of *complexity*. **Coefficient of determination R<sup>2</sup>:** - Percent variation explained. It ALWAYS increases the more complex the model. - Is is always zero for the **NULL** model. **log-likelihood `\(\log({\cal L})\)`:** - Total probability score of model. It ALWAYS increases the more complex the model. **Akaike Information Criterion:** - `\(AIC = -2 \log({\cal L}) + 2\,k\)` - A measure of model quality. - Smaller is better It starts getting bigger if the model complexity gets too high. - .red[**The lowest AIC value is the "best" model.**] - (but within 2 `\(\Delta AIC\)` is pretty much equivalent to best) ] --- background-image: url('images/AfricanUngulatesBiomass.png') background-size: cover ## AIC in action: **What predicts ungulate body size?** Quality (Nitrogen)? or Type (browse/grass)? --- background-image: url('images/GurarieSpringMigrations0.png') background-size: cover .pull-left-60[ <video width="100%" controls="controls"> <source src="https://terpconnect.umd.edu/~egurarie/research/ABoVE/springmigration/migrationanimation6.mp4"> </video> ] .pull-right-40[ ## Caribou spring migrations Remarkable temporal synchrony at a continental scale. ] --- background-image: url('images/GurarieSpringMigrations.png') background-size: cover ## Could the synchrony be driven by global weather drivers? .pull-right-70[ Pacific Decadal Oscillation, Arctic Oscillation, North Atlantic Oscillation: determine whether the winter is wet & snowy or dry & cold. ] --- background-image: url('images/GurarieSpringMigrations2.png') background-size: cover ## `\(\Delta\)`AIC Table 1: **Departure time** .pull-right[... driven by LARGE climate oscillations.] --- background-image: url('images/GurarieSpringMigrations3.png') background-size: cover ## `\(\Delta\)`AIC Table 2: **Arrival time** .pull-right[... completely independent of climate!] --- class: small .pull-left[ ## ***Step IV:*** *Generalized* linear modeling ### Normal Model .large[$$Y_i \sim {\cal Normal}(\alpha_0 + \beta_1 X_i, \sigma)$$] Models continuous data with a "normal-like" distribution. <!-- --> ] -- .pull-right[ ### Binomial model .large[$$Y_i \sim {\cal Bernoulli}\left( \frac{\exp(\alpha + \beta X_i)}{1 + \exp(\alpha + \beta X_i)} \right)$$] There's some *probability* of something happening that depends on the predictor `\(X\)`. **Bernoulli** just means the data are all 0 or 1. <!-- --> This models **presence/absence**, **dead/alive**, **male/female** other response variables with **2** possible outcomes. ] --- background-image: url('images/SoleaSolea.png') background-size: cover ### What factors predict occurence of *Solea solea* larvae? Sampled in the estuary of the Tejo river in Portugal - Lots of environmental factors in data .pull-right-70[.footnotesize[ <table class="table" style="margin-left: auto; margin-right: auto;"> <thead> <tr> <th style="text-align:right;"> depth </th> <th style="text-align:right;"> temp </th> <th style="text-align:right;"> salinity </th> <th style="text-align:right;"> transp </th> <th style="text-align:right;"> gravel </th> <th style="text-align:right;"> large_sand </th> <th style="text-align:right;"> fine_sand </th> <th style="text-align:right;"> mud </th> <th style="text-align:right;"> presence </th> </tr> </thead> <tbody> <tr> <td style="text-align:right;"> 3.0 </td> <td style="text-align:right;"> 20 </td> <td style="text-align:right;"> 30 </td> <td style="text-align:right;"> 15 </td> <td style="text-align:right;"> 3.74 </td> <td style="text-align:right;"> 13.15 </td> <td style="text-align:right;"> 11.93 </td> <td style="text-align:right;"> 71.18 </td> <td style="text-align:right;font-weight: bold;"> 0 </td> </tr> <tr> <td style="text-align:right;"> 2.6 </td> <td style="text-align:right;"> 18 </td> <td style="text-align:right;"> 29 </td> <td style="text-align:right;"> 15 </td> <td style="text-align:right;"> 1.94 </td> <td style="text-align:right;"> 4.99 </td> <td style="text-align:right;"> 5.43 </td> <td style="text-align:right;"> 87.63 </td> <td style="text-align:right;font-weight: bold;"> 0 </td> </tr> <tr> <td style="text-align:right;"> 2.6 </td> <td style="text-align:right;"> 19 </td> <td style="text-align:right;"> 30 </td> <td style="text-align:right;"> 15 </td> <td style="text-align:right;"> 2.88 </td> <td style="text-align:right;"> 8.98 </td> <td style="text-align:right;"> 16.85 </td> <td style="text-align:right;"> 71.29 </td> <td style="text-align:right;font-weight: bold;"> 1 </td> </tr> <tr> <td style="text-align:right;"> 2.1 </td> <td style="text-align:right;"> 20 </td> <td style="text-align:right;"> 29 </td> <td style="text-align:right;"> 15 </td> <td style="text-align:right;"> 11.06 </td> <td style="text-align:right;"> 11.96 </td> <td style="text-align:right;"> 21.95 </td> <td style="text-align:right;"> 55.03 </td> <td style="text-align:right;font-weight: bold;"> 0 </td> </tr> <tr> <td style="text-align:right;"> 3.2 </td> <td style="text-align:right;"> 20 </td> <td style="text-align:right;"> 30 </td> <td style="text-align:right;"> 15 </td> <td style="text-align:right;"> 9.87 </td> <td style="text-align:right;"> 28.60 </td> <td style="text-align:right;"> 19.49 </td> <td style="text-align:right;"> 42.04 </td> <td style="text-align:right;font-weight: bold;"> 0 </td> </tr> <tr> <td style="text-align:right;"> 3.5 </td> <td style="text-align:right;"> 20 </td> <td style="text-align:right;"> 32 </td> <td style="text-align:right;"> 7 </td> <td style="text-align:right;"> 32.45 </td> <td style="text-align:right;"> 7.39 </td> <td style="text-align:right;"> 9.43 </td> <td style="text-align:right;"> 50.72 </td> <td style="text-align:right;font-weight: bold;"> 0 </td> </tr> </tbody> </table> ]] --- # Presence of *Solea solea* against **salinity** .pull-left-40[ <!-- --> ] .pull-right-60[ Modeling is EXACTLY the same as **linear regression** except: - `glm` - for **generalized** linear model (instead of `lm`) - `family = 'binomial'` is the instruction to fit the logistic regression `glm(presence ~ salinity, family ='binomial')` <font size = 4> <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:right;"> Estimate </th> <th style="text-align:right;"> Std. Error </th> <th style="text-align:right;"> z value </th> <th style="text-align:right;"> Pr(>|z|) </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> (Intercept) </td> <td style="text-align:right;"> 2.661 </td> <td style="text-align:right;"> 0.902 </td> <td style="text-align:right;"> 2.951 </td> <td style="text-align:right;"> 0.003 </td> </tr> <tr> <td style="text-align:left;"> salinity </td> <td style="text-align:right;"> -0.130 </td> <td style="text-align:right;"> 0.035 </td> <td style="text-align:right;"> -3.716 </td> <td style="text-align:right;"> 0.000 </td> </tr> </tbody> </table> </font> Clearly - *Solea solea* presence is very significantly *negatively* related to salinity. ] --- ### Out of this model we can make predictions <img src="Lecture_Modeling_files/figure-html/unnamed-chunk-31-1.png" width="80%" /> --- .pull-left[ ## `\(\Delta\)`AIC analysis - and coefficients <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:left;"> Model </th> <th style="text-align:right;"> k </th> <th style="text-align:right;"> logLik </th> <th style="text-align:right;"> AIC </th> <th style="text-align:right;"> dAIC </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> M9 </td> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> salinity + gravel </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> -33.2 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 72.5 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;font-weight: bold;color: darkblue !important;background-color: yellow !important;"> 0.0 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> M2 </td> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> salinity </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 2 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> -34.3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 72.6 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 0.1 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> M7 </td> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> temp + salinity </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> -34.0 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 74.0 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 1.5 </td> </tr> <tr> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> M5 </td> <td style="text-align:left;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> depth + salinity </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> -34.1 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 74.3 </td> <td style="text-align:right;font-weight: bold;color: darkblue !important;background-color: lightgreen !important;"> 1.8 </td> </tr> <tr> <td style="text-align:left;"> M11 </td> <td style="text-align:left;"> depth + temp + salinity </td> <td style="text-align:right;"> 4 </td> <td style="text-align:right;"> -33.9 </td> <td style="text-align:right;"> 75.8 </td> <td style="text-align:right;"> 3.3 </td> </tr> <tr> <td style="text-align:left;"> M0 </td> <td style="text-align:left;"> depth </td> <td style="text-align:right;"> 2 </td> <td style="text-align:right;"> -38.1 </td> <td style="text-align:right;"> 80.1 </td> <td style="text-align:right;"> 7.6 </td> </tr> <tr> <td style="text-align:left;"> M4 </td> <td style="text-align:left;"> depth + temp </td> <td style="text-align:right;"> 3 </td> <td style="text-align:right;"> -38.0 </td> <td style="text-align:right;"> 81.9 </td> <td style="text-align:right;"> 9.4 </td> </tr> <tr> <td style="text-align:left;"> M6 </td> <td style="text-align:left;"> depth + gravel </td> <td style="text-align:right;"> 3 </td> <td style="text-align:right;"> -38.0 </td> <td style="text-align:right;"> 82.0 </td> <td style="text-align:right;"> 9.5 </td> </tr> <tr> <td style="text-align:left;"> M10 </td> <td style="text-align:left;"> depth + temp + gravel </td> <td style="text-align:right;"> 4 </td> <td style="text-align:right;"> -37.8 </td> <td style="text-align:right;"> 83.7 </td> <td style="text-align:right;"> 11.2 </td> </tr> <tr> <td style="text-align:left;"> M1 </td> <td style="text-align:left;"> temp </td> <td style="text-align:right;"> 2 </td> <td style="text-align:right;"> -43.3 </td> <td style="text-align:right;"> 90.6 </td> <td style="text-align:right;"> 18.1 </td> </tr> <tr> <td style="text-align:left;"> M3 </td> <td style="text-align:left;"> gravel </td> <td style="text-align:right;"> 2 </td> <td style="text-align:right;"> -43.7 </td> <td style="text-align:right;"> 91.3 </td> <td style="text-align:right;"> 18.8 </td> </tr> <tr> <td style="text-align:left;"> M8 </td> <td style="text-align:left;"> temp + gravel </td> <td style="text-align:right;"> 3 </td> <td style="text-align:right;"> -43.3 </td> <td style="text-align:right;"> 92.6 </td> <td style="text-align:right;"> 20.1 </td> </tr> </tbody> </table> ] .pull-right[ **Salinity** clearly among the more important covariates (in the top 4 models). 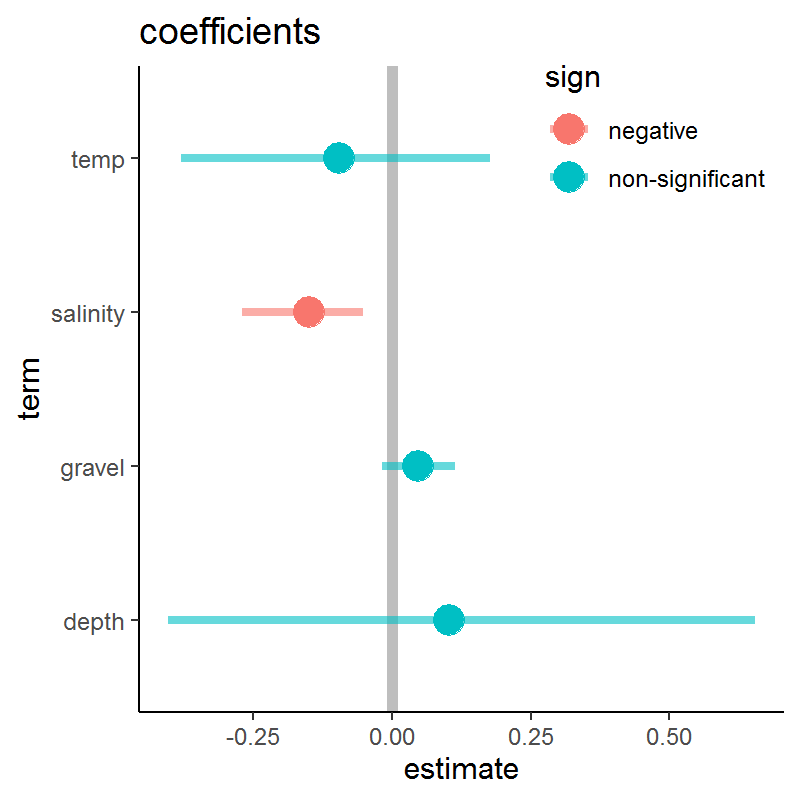<!-- --> ] --- background-image: url("images/RSF_dAIC.png") background-size: cover ## FLASHBACK: how the caribou Resource Selection Function was selected --- ## Poisson regression .pull-left-30[ 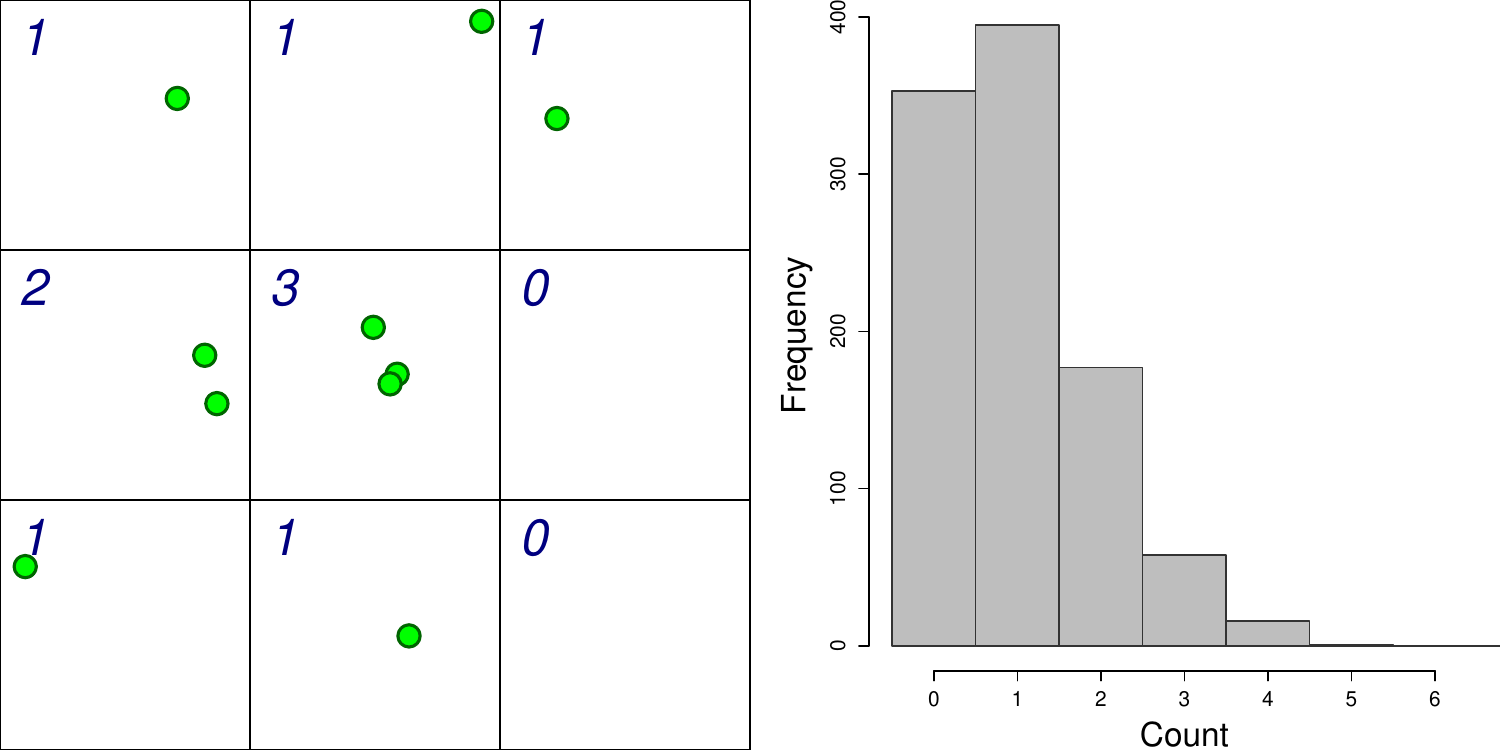 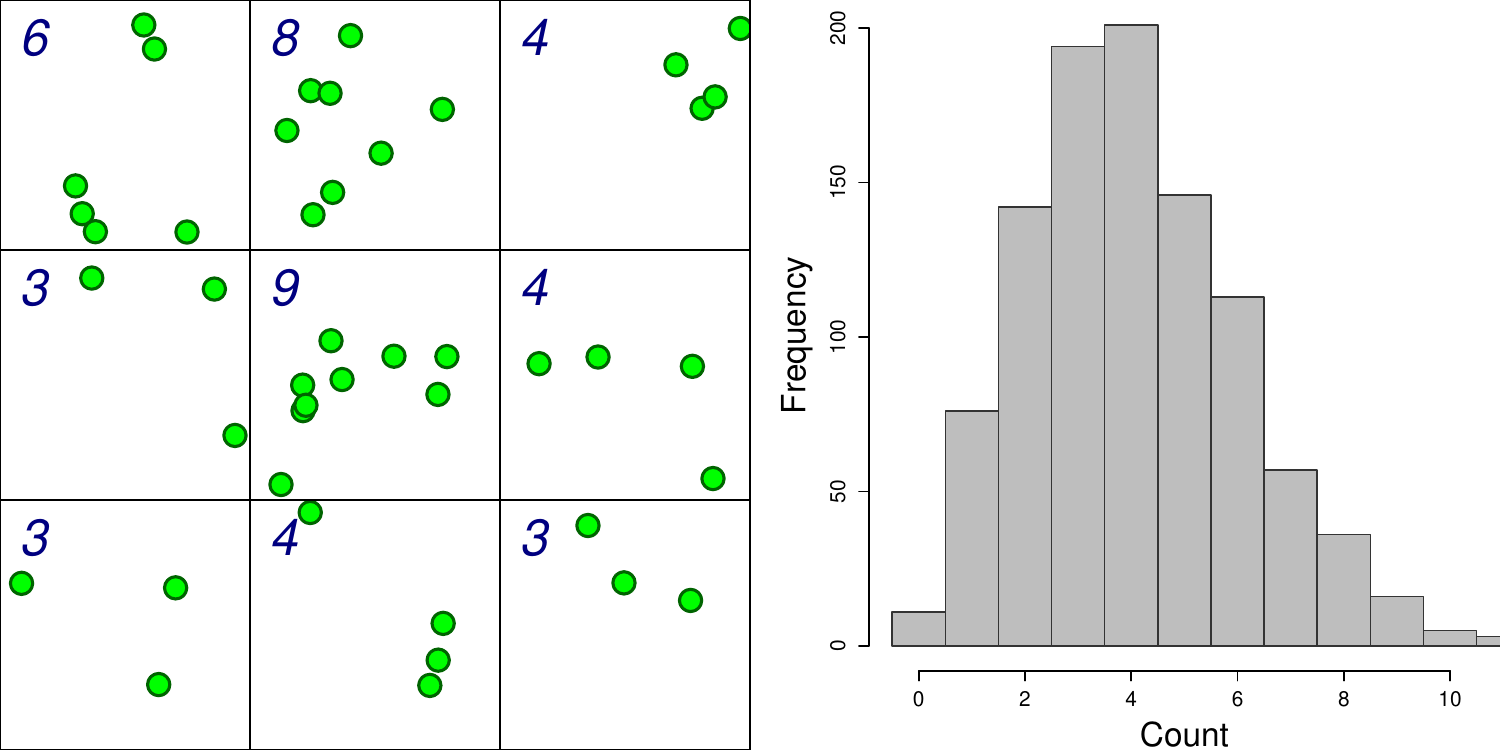  ] .pull-right-70[ .large[$$Y_i \sim {\cal Poisson}\left(\lambda = \exp(\alpha + \beta X_i) \right)$$] - We are **counting** something ... the data are between 0 and `\(\infty\)` - `\(\lambda\)` is a **density**; **densities** vary across habitat types (covariate **X**). .center[<img src='images/Moose2.png' width='70%'/>] ] --- ## Field flags .large[**Did flag densities vary with region?**] .pull-left-40[ Approximate areas: region | area --|-- **North:** | 82 m<sup>2</sup> **South:** | 82 m<sup>2</sup> **Perimeter:** | 196 m<sup>2</sup> --|-- **Sampling square (hula hoop)** | 0.5 m<sup>2</sup> ] .pull-right-60[ 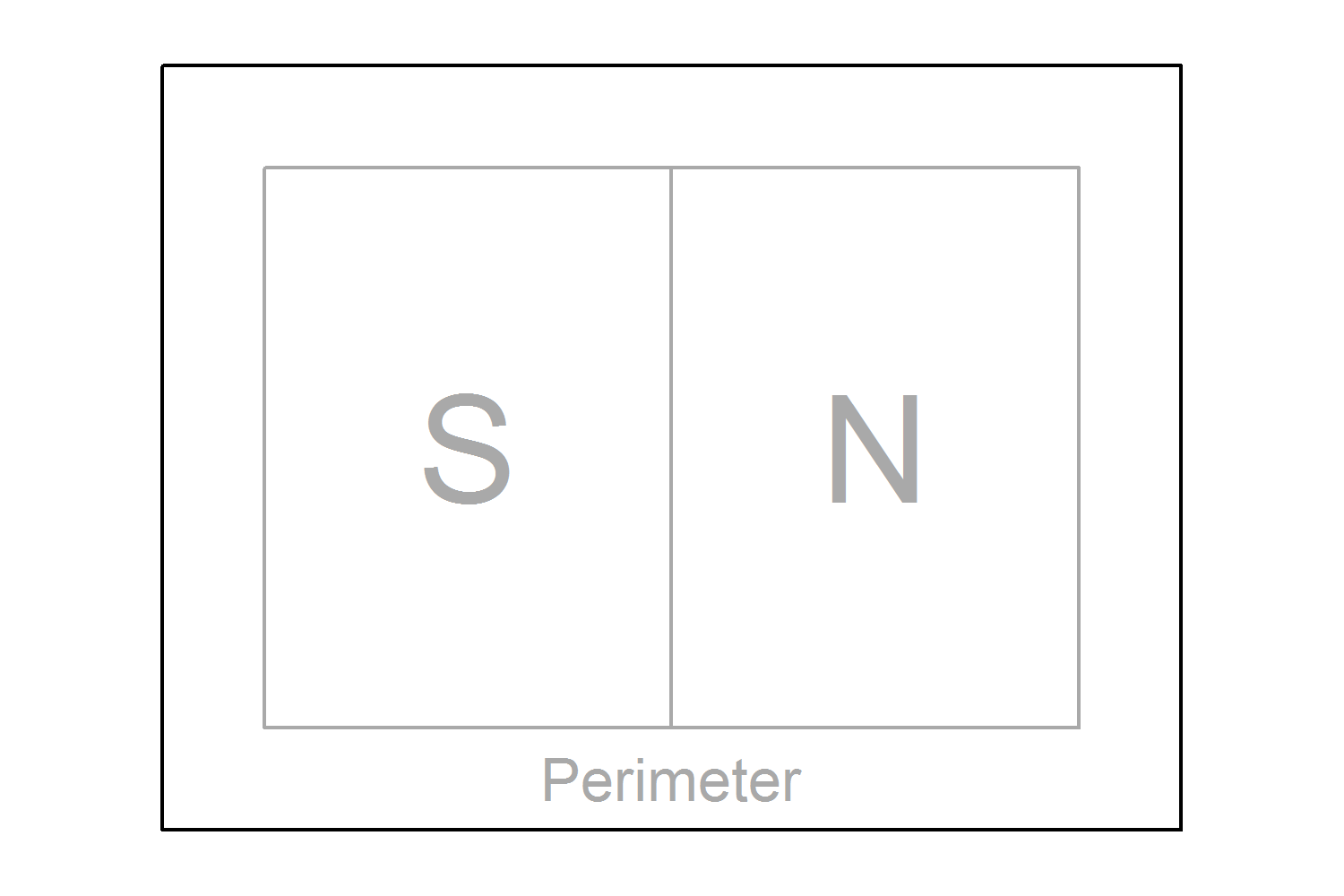] --- .pull-left[ ### Count data Lots of 0's, some 1's, and just one 2 count. ``` ## Region ## Count North Perimeter South ## 0 15 12 9 ## 1 1 1 6 ## 2 0 0 1 ``` <!-- --> ] .pull-right[ ### Fitting models .large[ `glm(count ~ region, family = 'poisson')` Exact same syntax as before, except the "family" is **Poisson.** ]] --- .pull-left[ ### Count data Lots of 0's, some 1's, and just one 2 count. ``` ## Region ## Count North Perimeter South ## 0 15 12 9 ## 1 1 1 6 ## 2 0 0 1 ``` <!-- --> ] .pull-right[ ### Fitting models <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:right;"> Estimate </th> <th style="text-align:right;"> Std. Error </th> <th style="text-align:right;"> z value </th> <th style="text-align:right;"> Pr(>|z|) </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> (Intercept) </td> <td style="text-align:right;"> -2.773 </td> <td style="text-align:right;"> 1.000 </td> <td style="text-align:right;"> -2.773 </td> <td style="text-align:right;"> 0.006 </td> </tr> <tr> <td style="text-align:left;"> RegionPerimeter </td> <td style="text-align:right;"> 0.208 </td> <td style="text-align:right;"> 1.414 </td> <td style="text-align:right;"> 0.147 </td> <td style="text-align:right;"> 0.883 </td> </tr> <tr> <td style="text-align:left;"> RegionSouth </td> <td style="text-align:right;"> 2.079 </td> <td style="text-align:right;"> 1.061 </td> <td style="text-align:right;"> 1.961 </td> <td style="text-align:right;"> 0.050 </td> </tr> </tbody> </table> The **intercept** here is "North", the *p*-values compare with North. So **South** has - borderline - significantly more #### `\(\Delta AIC\)` table <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:right;"> df </th> <th style="text-align:right;"> AIC </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Null.model </td> <td style="text-align:right;"> 1 </td> <td style="text-align:right;"> 53.47 </td> </tr> <tr> <td style="text-align:left;"> Region.model </td> <td style="text-align:right;"> 3 </td> <td style="text-align:right;"> 49.15 </td> </tr> </tbody> </table> Model that includes **Region** has lower AIC ] --- ### Making predictions <table> <thead> <tr> <th style="text-align:left;"> Region </th> <th style="text-align:right;"> area </th> <th style="text-align:right;"> fit </th> <th style="text-align:right;"> se.fit </th> <th style="text-align:right;"> l.hat </th> <th style="text-align:right;"> l.low </th> <th style="text-align:right;"> l.high </th> <th style="text-align:right;"> d.hat </th> <th style="text-align:right;"> d.low </th> <th style="text-align:right;"> d.high </th> <th style="text-align:right;"> N.hat </th> <th style="text-align:right;"> N.low </th> <th style="text-align:right;"> N.high </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> South </td> <td style="text-align:right;"> 82 </td> <td style="text-align:right;"> -0.693 </td> <td style="text-align:right;"> 0.354 </td> <td style="text-align:right;"> 0.500 </td> <td style="text-align:right;"> 0.247 </td> <td style="text-align:right;"> 1.014 </td> <td style="text-align:right;"> 1.000 </td> <td style="text-align:right;"> 0.493 </td> <td style="text-align:right;"> 2.028 </td> <td style="text-align:right;"> 82.0 </td> <td style="text-align:right;"> 40.4 </td> <td style="text-align:right;"> 166.3 </td> </tr> <tr> <td style="text-align:left;"> North </td> <td style="text-align:right;"> 82 </td> <td style="text-align:right;"> -2.773 </td> <td style="text-align:right;"> 1.000 </td> <td style="text-align:right;"> 0.063 </td> <td style="text-align:right;"> 0.008 </td> <td style="text-align:right;"> 0.462 </td> <td style="text-align:right;"> 0.125 </td> <td style="text-align:right;"> 0.017 </td> <td style="text-align:right;"> 0.924 </td> <td style="text-align:right;"> 10.2 </td> <td style="text-align:right;"> 1.4 </td> <td style="text-align:right;"> 75.8 </td> </tr> <tr> <td style="text-align:left;"> Perimeter </td> <td style="text-align:right;"> 196 </td> <td style="text-align:right;"> -2.565 </td> <td style="text-align:right;"> 1.000 </td> <td style="text-align:right;"> 0.077 </td> <td style="text-align:right;"> 0.010 </td> <td style="text-align:right;"> 0.568 </td> <td style="text-align:right;"> 0.154 </td> <td style="text-align:right;"> 0.021 </td> <td style="text-align:right;"> 1.137 </td> <td style="text-align:right;"> 30.2 </td> <td style="text-align:right;"> 4.1 </td> <td style="text-align:right;"> 222.9 </td> </tr> </tbody> </table> .small[ - **fit** and **se.fit** are in the log scale, so they need to be transformed via `\(exp\)` to intensities `\(\lambda\)`. - `l.hat` is the Poisson intensity `\(\lambda\)` of the sampling square (**hula hoop**), which we turn into an actual density by dividing by its area **0.5 m<sup>2</sup>**. - `d.hat` (and `d.low` and `d.high`) are the density estimates & confidence intervals, which we then turn into our numerical predictions by multiplying by area. ] ### Total estimate .large.green[ `$$\widehat{N} = 122.4 \, (95\%\, \text{C.I.}: 71.4 - 173.4)$$` ] **pretty darned good!** The true values were 92 total [58 S, 29 N, 13 perimeter] --- background-image: url('images/LEGO.jpg') background-size: cover .content-box-blue[ ## .darkred[**Take-aways on (linear, statistical) modeling**] 1. **Linear modeling** separates **patterns** (the model) from "**randomness**" (unexplained variation). 2. We structure our models to have a **response variable** and one or more **predictors** or **covariates**. 3. Depending on the reponse variable, a different **family** is chosen: - if **continuous** and symmetric: **Normal** family - if two values (presence/absence, dead/alive): **Binomial** family - if count data: **Poisson** family. 3. An important task is **Model selection**, identifying which model is "best" - Best means *"explains the most variation without overfitting"* - Very common criterion is **AIC.** 4. Once a model is "selected", we can: - analyze the results by seeing the **effect sizes** (magnitude of coefficients, aka *slopes*) and **directions** (signs of coefficients) - make **inferential predictions** by "spreading" our model over a larger landscape. 6. **Well over 90% of habitat modeling is done this way!** ] --- # extra slides --- # Some comments on linear models $$ Y_i \sim \alpha + \beta X_i + \epsilon_i$$ 1. `\(\epsilon_i\)` is **unexplained variation** or **residual variance**. It is often POORLY/WRONGLY referred to as "**error**". It is a **random variable**, NOT a **parameter** -- 2. A **better**, more sophisticated way to think of this model is not to focus on isolating the residual variance, but that the whole process is a random variable: `$$Y_i \sim {\cal N}(\alpha + \beta X_i, \sigma)$$` This is better because: (a) the three parameters ( `\(\alpha, \beta, \sigma\)` ) are more clearly visible, (b) it can be "generalized". For example the **Normal distribution** can be a **Bernoulli distribution** (for binary data), or a **Poisson distribution** for count data, etc. -- 3. `\(\alpha+\beta X_i\)` is the **predictor**, or the "modeled" portion. There can be any number of variables in the **predictor** and they can have different powers, so: `$$Y_i \sim {\cal N}(\alpha + \beta X_i + \gamma Z_i + \delta X_i^2 + \nu X_i Z_i, \sigma )$$` is also a **linear** model.