class: left, title-slide .title[ # .white[Counting Animals Part II: Sample Counts] ] .subtitle[ ## .white[EFB 390: Wildlife Ecology and Management] ] .author[ ### .white[Dr. Elie Gurarie] ] .date[ ### .white[September 12, 2024] ] --- <!-- https://bookdown.org/yihui/rmarkdown/xaringan-format.html --> ## Drawbacks of total counts / censusing .pull-left-60.large[ Expensive & labor-time intensive Impractical for MOST species / systems - need to ALL be **visible** - the **ENTIRE** study area needs to be survey-able Hard to assess precision ] .pull-right-40[  .center[**Hippos**] .small.grey[(Marc Mol/Mercury Press/Caters)] ] --- ### Is the great Elephant Census a Census? <iframe src="https://www.youtube.com/embed/imvehfydUpc?controls=0" width="900px" height="500px"> </iframe> --- class: inverse # Sample counts ### Simple idea: - count *some* of the individuals - extrapolate! -- ### In practice: - Necessarily - less **precise** due to **sampling error**. - BUT, if properly done, more **accurate** and **much less effort**. - Involves some (tricky) *statistics* and *modeling!* ### By Necessity: **Very Common** --- ## A random population .pull-left-60[  ] -- .pull-right-40[ ### Population density .large[$$N = A \times D$$] - `\(N\)` - total count - `\(A\)` - total area - `\(D\)` - overall density ] .red[***Which of these do we know?***] --- ## Sampling from the population .pull-left-60[  .center[**Squares**, aka, **quadrats**] ] -- .pull-right-40[ ### *Sample* density: `$$n_{sample} = \sum_{i=1}^k n_i$$` `$$a_{sample} = \sum_{i=1} a_i$$` `$$d_{sample} = {n_{sample} \over a_{sample}}$$` ] --- ### Sample vs. Population | Population | Sample --|:--:|:-- size | `\(N\)` | `\(n_s\)` area | `\(A\)` | `\(a_s\)` density | `\(D\)` | `\(d_s\)` "sample density" `\(d_s\)` is an *estimate* (guess) of total density: `$$\widehat{D} = d_s$$` -- ### True population: .green.large[$$N = A \times D$$] Population **estimate** (best guess for `\(N\)`): just replace true (unknown) density `\(D\)` with *sampling estimate* of density `\(d_s\)`: .red.large[$$\widehat{N} = A \times \widehat{D} = A \times d_s = A \times {n_s \over a_s}$$] --- .pull-left[ ## Example  ] ### Data .blue[10 quadrats; 10x10 km each] .blue[ `n = {0,0,5,0,3,1,2,3,6,1}`] .red[**note:** *variability / randomness!*] -- .pull-right[ ### Analysis .green[ `\(n_s = \sum n_i = 21\)` `\(d_s = \widehat{D} = {21 \over 10 \times 10 \times 10} = 0.021\)` `\(A = 100 \times 100\)` ] ] -- #### final estimate: .Large.green[ `$$\widehat{N} = \widehat{D} \times A = 100\times100\times0.021 = \textbf{210}$$`] --- ## What happens when we do this many times? .pull-left[  ] .pull-right[ Every time you do this, you get a different value for `\(\widehat{N}\)`.  ] --- ### Statistics .pull-left[ **Mean of estimates:** `$$\widehat{N} = 301.5$$` **S.D. of estimate:** `$$s_{\widehat{N}} = 54.6$$` .red[**important**: the *standard deviation* of an *estimate* = **standard error**, SE] **95% Confidence Interval:** `$$\widehat{N} \pm 1.96 \times SE = \{195-408\}$$` .green[**note:** the 1.96 is the number of standard deviatinos that captures 95% of a Normal distribution.] ] .pull-right[  ] -- Conclusion: this estimate is **accurate** (unbiased), but not very **precise** (big confidence interval). --- ## Estimating **precision** of the estimate **v. 1** **IF:** `1.` Total area covered is small: `\(a_s \ll A\)` - (.green[.small[*Fryxell says < 15% coverage*]]) `2.` **OR** You are potentially resampling the same individuals - (.green[.small[*Fryxell calls this* ***Sampling With Replacement*** [SWR]]]) `3.` **And** samples are .blue[*distributed throughout the range*] - (.green.small[this is a BIG assumption, we will revisit]) then: .darkred[$$SE(\widehat{N}) = A {\sqrt{\sum n_i} \over ak}$$] - `\(n_i\)` is set of **sample counts** - `\(k\)` is the **number of samples**: `\(i =\{1,2,...,k\}\)` ) - `\(a\)` is the area of the sample frame ] **Much uglier!** but this formula takes into account the actual *variability* among the counts correctly. --- ## In our example .Large.darkred[$$SE(\widehat{N}) = A {\sqrt{\sum n_i} \over ak}$$] - `\(n_i\)` is set of **sample counts** - `\(k\)` is the **number of samples**: `\(i =\{1,2,...,k\}\)` ) - `\(a\)` is the area of the sample frame raw counts were `n = {0,0,5,0,3,1,2,3,6,1}` .pull-left[ quantity | value ---|--- a | 10 A | 100² k | 10 `\(\sum n\)` | 21 ] .pull-right.darkred[ `$$\begin{align} SE &= 100² \times {\sqrt{21} \over 100 \times 10}\\ &= {\huge 54.8} \end{align}$$` ] --- ## Estimating **precision** of the estimate **v. 2** **IF:** `1.` Total area covered is small: `\(a_s \ll A\)` - (.green[.small[*Fryxell says < 15% coverage*]]) `2.` **OR** You are potentially resampling the same individuals - (.green[.small[*Fryxell calls this* ***Sampling With Replacement*** [SWR]]]) `3.` **And** samples are .blue[*you don't knoe how they are distributed throughout the range*] - (.green.small[this is a MUCH BETTER assumption]) then: .darkred[ `$$SE(\widehat{N}) = {A \over ka} \sqrt{ {\sum n_i^2 - (\sum n_i)^2/k) \over k(k - 1)}}$$` ] .center[**Much uglier! But more useful!**] --- ## In our example .Large.darkred[$$SE(\widehat{N}) = A \sqrt{ {\sum n_i^2 - (\sum n_i)^2/k) \over k(k - 1)}}$$] raw counts: `n = {0,0,5,0,3,1,2,3,6,1}` .pull-left-40[ quantity | value ---|--- a | 10 A | 100² k | 10 `\(\sum n^2\)` | 85 `\((\sum n)^2\)` | 441 ] .pull-right-60[ ``` r n = c(0,0,5,0,3,1,2,3,6,1) a <- 10; A <- 100^2; k <- 10 (A/(k*a) * sqrt( (sum(n^2) - (sum(n)^2/k)) / (k*(k-1)) )) ``` ``` ## [1] 67.41249 ``` .large.center.darkred[ `\(SE(\widehat{N}) = 67.4\)` ] ] --- class: inverse ## In-class Experiment #### Some facts - There are **62** students in this class. - Each student has a first name, composed of some number *n* of letters - There are a total of .red[***N***] letters in all the first names of the class. #### The challenge: - break into groups of **8-12** and record the number of letters in the first names of all the people in your group - estimate the total number of letters in the names of the entire class. #### formulae .center.red[ `\(\widehat{N} = A {\sum n \over ak}; \,\,\,\,\, SE(\widehat{N}) = A \sqrt{ {\sum n_i^2 - (\sum n_i)^2/k) \over k(k - 1)}}\)` ] --- # Combining estimates .pull-left[ If you have multiple sub-count estimates (e.g. one for each of `\(r\)` sub-region): .darkred[ - `\(\widehat{N_1}, \widehat{N_2}, ..., \widehat{N_r},\)` ] and each estimate has a standard error: .darkred[ - `\(SE(\widehat{N_1}), SE(\widehat{N_2}), ..., SE(\widehat{N_r})\)` ] Then ... ] -- .pull-right[ ... the **total** estimate will be: .darkgreen[ `$$\widehat{N} = \sum_{i = 1}^r \widehat{N_i}$$` ] and the standard error will be: .darkgreen[ `$$SE(\widehat{N}) = \sqrt{\sum_{i = 1}^r SE(\widehat{N_i})^2}$$` ] ] -- .red.center[*Is this estimate more precise?*] --- ## Some other formulae from Fryxell book Chapter 12:  These are used when **sampling areas** are unequal, and account for differences when sampling **with replacement** or **without replacement**. --- ### Poisson process Models *counts*. If you have a perfectly random process with mean *density* (aka *intensity*) 1, you might have some 0 counts, you might have some higher counts. The *average* will be 1:  --- ### Poisson process Here, the intensity is 4 ...  --- ### Poisson process ... and 10. Note, the bigger the intensity, the more "bell-shaped" the curve.  Here's the formula of the Poisson Distribution: `\(\!f(k; \lambda)= \Pr(X{=}k)= \frac{\lambda^k e^{-\lambda}}{k!}\)` --- ### Poisson distribution holds if process is truly random ... not **clustered** or **inhibited**  If you **sample** from these kinds of spatial distributions, your standard error might be smaller (*inhibited*) or larger (*clustering*). This is called *dispersion*. --- ### Also ... densities of animals depend on habitat! .pull-left-60[ **Wolf habitat use**  ] .pull-right-40[ If you look closely: - No locations in lakes - Relatively few in bogs / cultivated areas. - Quite a few in mixed and coniferous forest ] --- ## Imagine a section of forest ... .pull-left-60[ ] --- ## ... with observations of moose .pull-left-60[ ] .pull-right-40[ **How can we tell what the moose prefers?** Habitat | Area | n | Density ---:|:---:|:---:|:--- open | 100 | 21 | 0.21 mixed | 100 | 43 | 0.43 dense | 200 | 31 | 0.16 **total** | 400 | 95 | 0.24 ] .blue[Knowing how densities differ as a function of **covariates** can be very important for generating estimates of abundances, increasing both **accuracy** and **precision**, and informing **survey design**.] --- ### Sample frames need not be **squares** .pull-left-50[  ] .pull-right-50[ ## Transects Linear strip, usually from an aerial survey. Efficient way to sample a lot of territory. If "perfect detection", referred to as a **strip transect**. Statistics - essentially - identical to quadrat sampling. ] .footnote[https://media.hhmi.org/biointeractive/click/elephants/survey/survey-aerial-surveys-methods.html] --- ### **Stratified sampling** for more efficient estimation 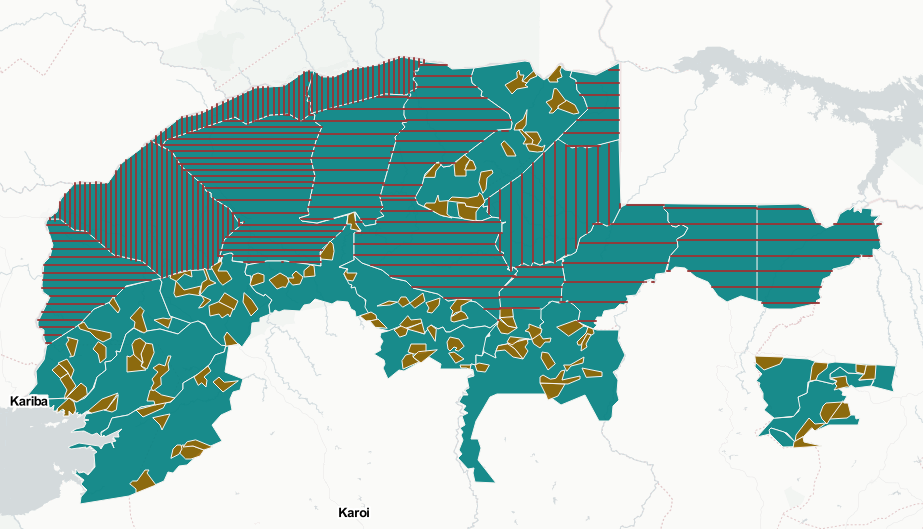 Sample more intensely in those habitats where animals are more likely to be found. Intensely survey .orange[**blocks**] where detection is more difficult. .footnote[https://media.hhmi.org/biointeractive/click/elephants/survey/survey-aerial-surveys-methods.html] --- ### **Stratified sampling** for more efficient estimation 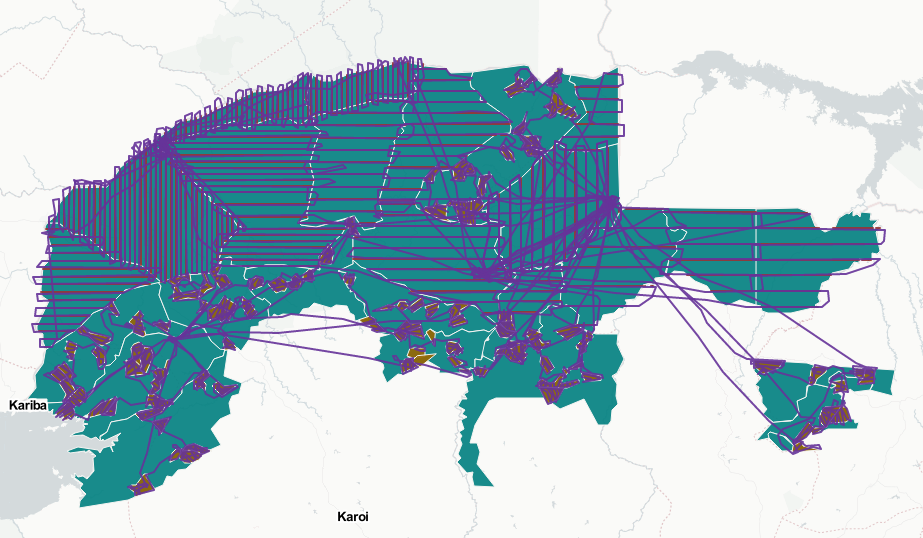 Actual elephant flight paths, .footnote[https://media.hhmi.org/biointeractive/click/elephants/survey/survey-aerial-surveys-methods.html] --- ### **Stratified sampling** .pull-left[] .pull-right[] **Stratification** is used to optimize **effort** and **precision**. Aircraft cost thousands of dollars per hour! (In all of these comprehensize surveys - *design* takes care of **accuracy**). --- ### Sampling strategies .pull-left[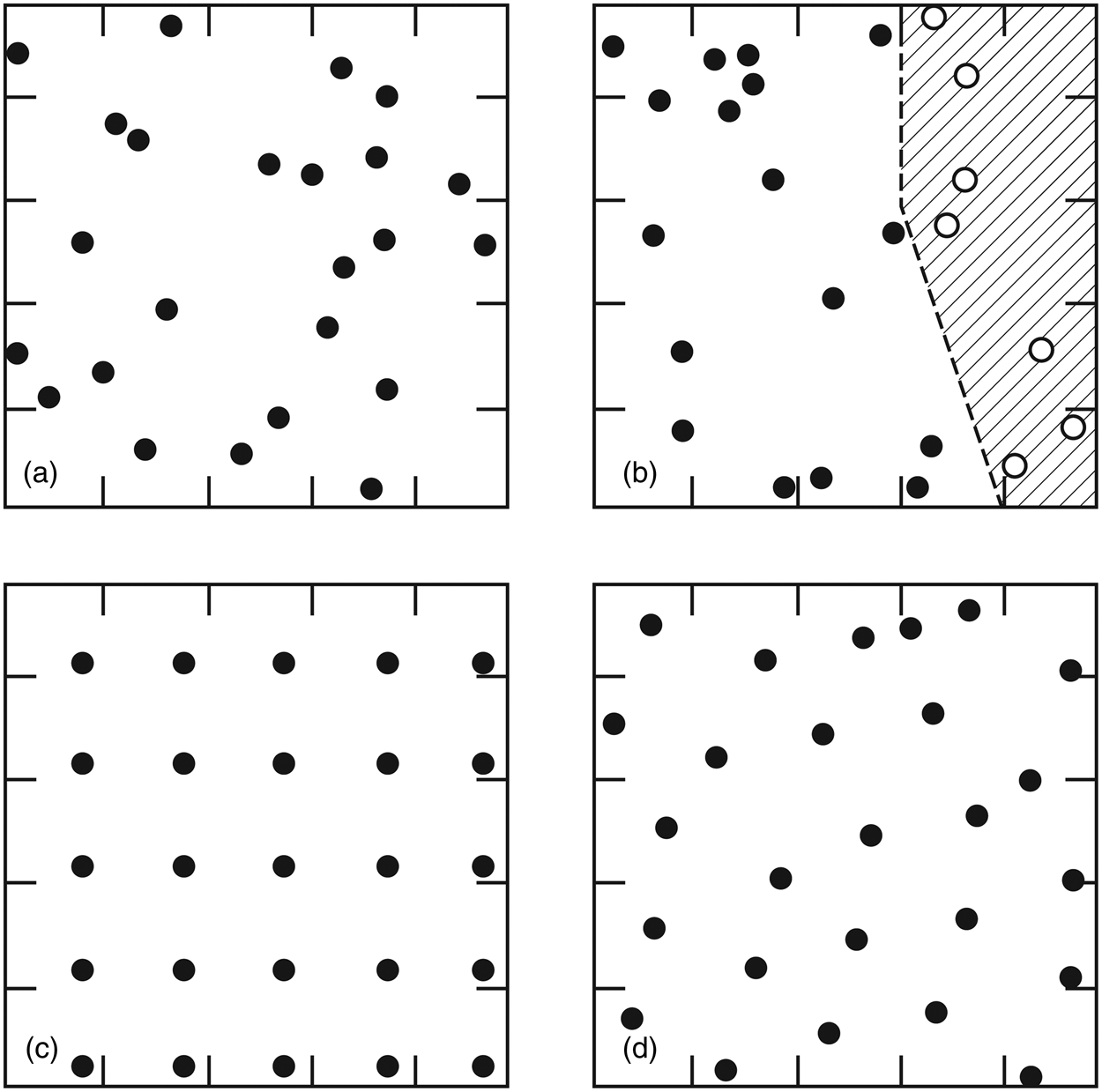] .pull-right[ (a) simple random, (b) stratified random, (c) systematic, (d) pseudo-random (systematic unaligned). Each has advantages and disadvantages. See also: *Adaptive Sampling* ] --- ### Detections usually get *worse* with distance! .pull-left-30[   ] .pull-right-70[ ## Distance Sampling The statistics of accounting for visibility decreasing with distance 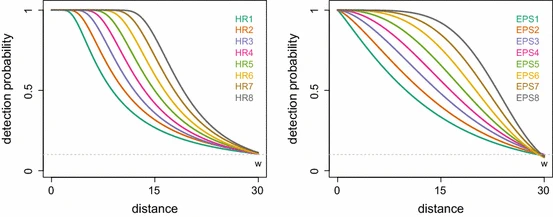 ] --- ## Example reindeer in Svalbard  .large[ **Estimated detection distance**, compared to **total count**, incorporated **vegetation modeling**, computed **standard errors**, concluded that you can get a 15% C.V. for 1/2 the cost.] --- ## Example Ice-Seals  --- ## Example: Flag Counting at Baker  --- ## Nice video on counting caribou https://vimeo.com/471257951