Limits on Population Growth

class: center, top, title-slide

.title[
# <strong>Limits on Population Growth</strong>
]
.subtitle[
## .white[EFB 390: Wildlife Ecology and Management]
]
.author[
### <strong>Dr. Elie Gurarie</strong>
]
.date[
### October 28, 2025
]

---

.pull-left-70[
---
## As populations grow ...

### they always hit **Limits to growth**

.content-box-blue.large[
- Space limits

- Resource limitations

- Competition

- Predation

- Disease

*All of these can interact *
]
]

.pull-right-30[
![](images/limits.jpg)
]

---

## Fundamental population equation

`$$\huge \Delta N = B - D + I - E$$`
.large[

Exponential growth assumes these (especially .red[**Birth**] & .red[**Death**]) are proportional to .red[**N**].

(in other words, *per capita* death *d* and birth *b* rates are constant)

But at high N ... B can fall, or D can rise, or I can decrease or E can increase.

]

### Density dependence

.large[
Means that the *rate* of a parameter(e.g. `$b = {B\over N}$` or `$d = {D\over N}$` is: 
- (a) NOT constant
- (b) dependent on total population (or density) `$N$`.  
]

---

## Key demographic rates: **Fecundity** & **Survival**

.pull-left[

### Fecundity

**Number of offspring produced per individual** (usually per female)

.content-box-blue[
**Notation:**
- `$b$` = fecundity rate
- `$B = b \times N$` (total births)
- Often measured as:
  - offspring per female per year
  - litter size × litters per year
]

**Examples:**
- White-tailed deer: ~1.5 fawns/female/year
- Wolves: ~4 pups/female/year (in a pack)
- Mice: 5-10 pups/litter, multiple litters/year

]

.pull-right[

### Survival | Mortality

**Probability an individuals survives | dies**

.content-box-blue[
**Notation:**
- `$s$` = survival rate (proportion surviving)
- `$d = 1-s$` death rate
- `$D = d \times N$` (total deaths)
]

**Examples:**

- Adult deer: `$s \approx 0.85$` (85% survive/year)
  - equivalently: `$d \approx 0.15$` (15% die/year)
- Juvenile survival often much lower
- Can vary by age, sex, season

]

---

.pull-left-50[
## Example: Wolf populations

-	Dispersal into new area, mainly wolf mating pairs. 
-	Highly territorial! 
-	Wolves produce up to 4 pups per litter that survive
-	If there are no neighbors, wolves will disperse to found new packs
-	Pack with 8 adults or 2 adults, still produces (about) 4 pups per litter 
-	If there are lots of neighbors, packs become larger (more individuals) in smaller territories.

]

.pull-right-50[

**Expansion of Wisconsin Wolves, 1970's to 2000's**

![](images/WI_WolfTerritories.png)
]

---

##  Human-wolf experiment model

.pull-left-60[

### basics of model
- 8 possible territories
- 1 initial dispersing wolf (female)

### each season ...
- One female / pack gives birth to 2 offspring
- Offspring can choose whether to disperse or not 
- 1/4 of all wolves die each year
]

.pull-right-40[
![](images/wolfmother.jpg)
]

Enter data [here](https://docs.google.com/spreadsheets/d/15j2b3FCfbtrPkAlRb6QE6s55aRqggeSDi5YU6OBh7Yc/edit?usp=sharing)

---
class: inverse

##  Results of Human Wolf Experiment

.center[![](images/PackPopulationOverTime.png)

Looks a lot like initial exponential growth stabilizes around 20 ind as die-offs balance out births. 
]

---

.pull-left[

# Modeling wolf population

Population equation:

`$$N_t = (1 + b - d) \times N_{t-1}$$`

Death rate is constant: `$d = 0.25$`

Birth rate is high when population is low:
`$b_0 = 2$`

Birth rate is small when population is high:
- `$N = 1$`; `$B = 2$`; `$b = 2$`
- `$N = 8$`; `$B = 16$`; `$b = 2$`

But it hits an absolute maximum of 16 total.  So if:
- `$N = 32$`; `$B = 16$`; `$b = 1/2$`
- `$N = 64$`; `$B = 16$`; `$b = 1/4$`

]

.pull-right-40[

![](Lecture_PopulationEcology_PartII_files/figure-html/WolfLogisticGrowth-1.png)

]

---

.pull-left-60[

##  Some Concepts

- Natural populations are always eventually limited

- The "cap" on a population is called the .darkred[***Carrying Capacity*** ] (symbol: **K**).  This is

- When population rates (*b*, *d*, also *i*, *e*) depend on the **total population**, this is called: .darkred[***Density Dependence***].

- The maximum growth rate (max `$b-d$`) is called the .darkred[**intrinsic growth rate**].

]

.pull-right-40[

![](Lecture_PopulationEcology_PartII_files/figure-html/WolfLogisticGrowth_II-1.png)

]

---

.pull-left[

# Logistic growth

.darkred[***Logistic growth***] is a specific kind of .darkred[Density Dependent] growth where the relationship between ***r*** and ***N*** is .darkred[**linear**]. The formula is:
`$$r = r_0 (1 - N/K)$$`

]

.pull-right[

![](Lecture_PopulationEcology_PartII_files/figure-html/logisticcurves-1.png)

- At `$N=0$` - growth = 0
- At `$N$` slightly above 0 - growth maximum `$\approx r_0$`
- At `$N = K$` - growth = `$0$`
- At `$N > K$` - growth < `$0$`
]

---

## Exponential vs. Logistic Growth in Three Graphs

.pull-left[
  ***Exponential*** | ***Growth***
  ---:|:---
  equation: | `${dN \over dt} = r N$`
  solution: | `$N(t) = N_0e^{rt}$`
]

.pull-right[
  ***Logistic*** | ***Growth***
  ---:|:---
  equation: | `${dN \over dt} = r_0 N\left(1-{N\over K}\right)$`
  solution: | `$N(t) = {K \over 1 + \left({K-N_0 \over N_0}\right)e^{-r_0 t}}$`
]

<br>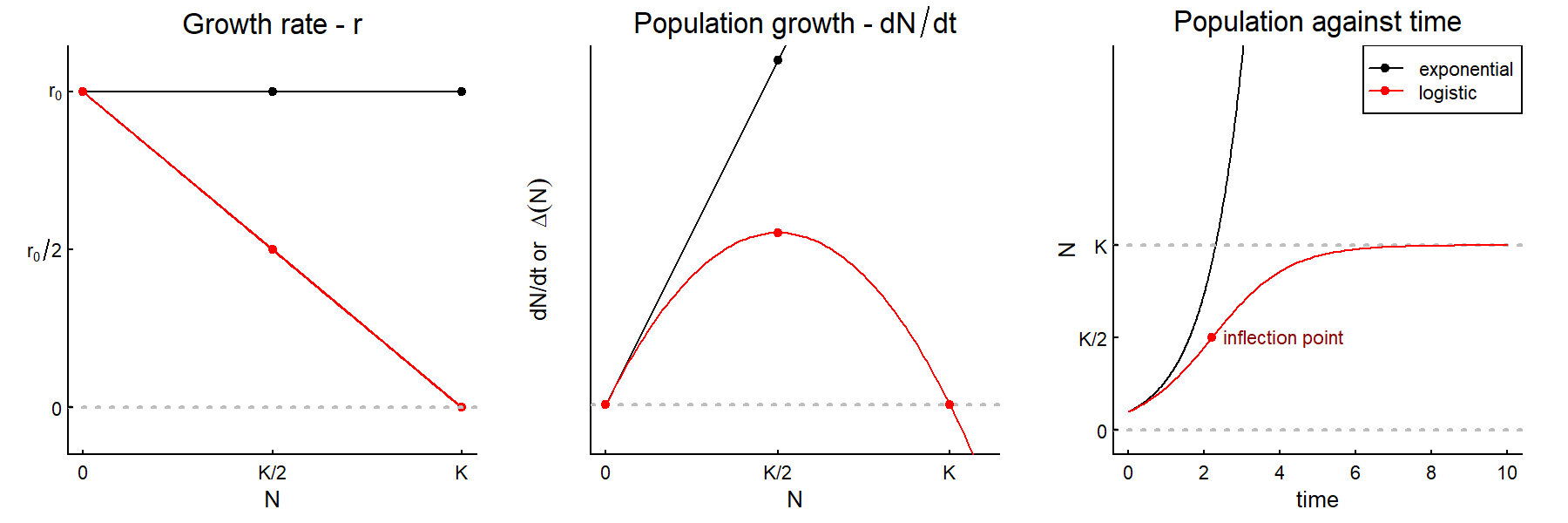
![](images/ThreeFigures2-1.png)

---

## Intrinsic growth rate:  `$r_0$`
.pull-left-40[
***In the best of all possible worlds***

.large[
`$$\large r_0 = 1.5 \, W^{-0.36}$$`
]

`$W$` is live weight in kilograms
<table class="table table-striped" style="font-size: 16px; color: black; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> Species </th>
   <th style="text-align:right;"> Weight (kg) </th>
   <th style="text-align:right;"> r₀ </th>
   <th style="text-align:right;"> Doubling time (years) </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> Mouse </td>
   <td style="text-align:right;"> 0.02 </td>
   <td style="text-align:right;"> 6.13 </td>
   <td style="text-align:right;"> 0.1 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> White-tailed Deer </td>
   <td style="text-align:right;"> 60 </td>
   <td style="text-align:right;"> 0.34 </td>
   <td style="text-align:right;"> 2.0 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Elephant </td>
   <td style="text-align:right;"> 4000 </td>
   <td style="text-align:right;"> 0.08 </td>
   <td style="text-align:right;"> 8.7 </td>
  </tr>
</tbody>
</table>

**Q. Why would this be the case?**

.large[Smaller animals: shorter generation times, larger litters, faster maturation]

]

.pull-right-60[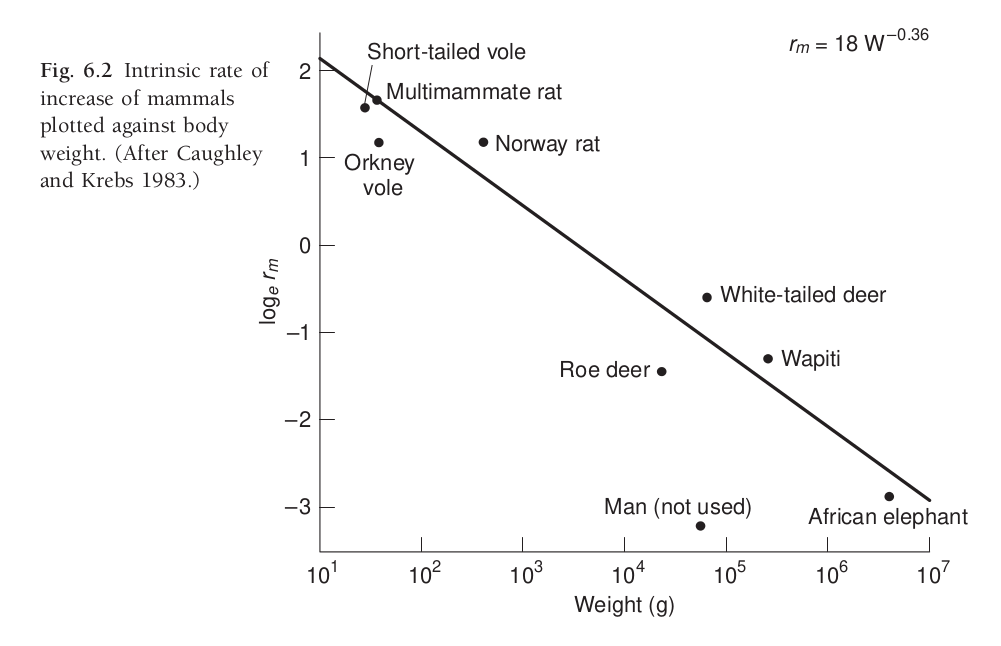

![](images/IntrinsicGrowthRates_trimmed.png)

.small.center[[Caughley and Krebs (1983)](https://www.zoology.ubc.ca/~krebs/papers/58.pdf)
]

]

---

## Different models of density dependence

.pull-left-30[

**What is it that depends on density?**

Is it birth?  Is it death?  Is it linear?  Is it curvy?

]

.pull-right-70[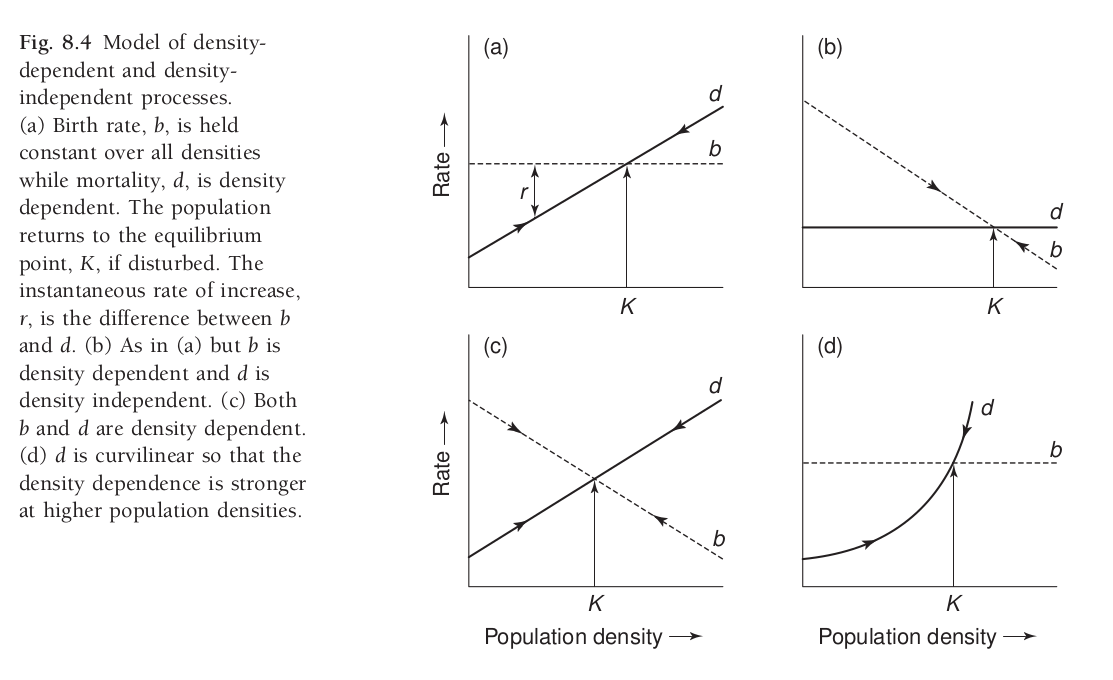
![](images/DensityDependence.png)

.center[Fryxell chapter 8.]
]

---

# Density dependent mortality & fecundity

.pull-left-30[
## Convex curves

- **Mortality** can be high when densities are highest.

- **Fecundity** (# of offspring per female) falls at high densities.

- For long-lived animals, this effect mainly kicks in at high numbers (*not linear*).  
]

.pull-right-70[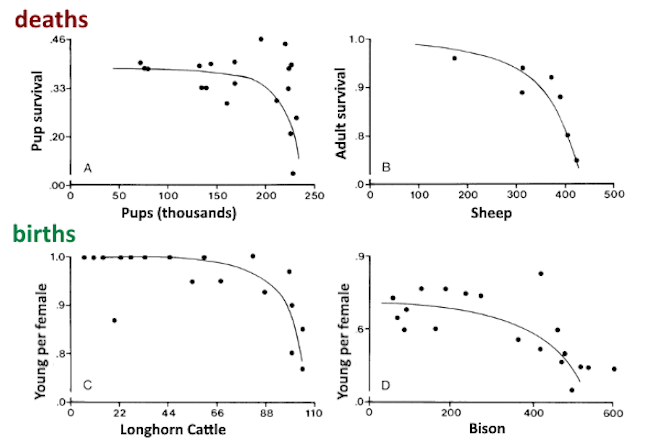
![](images/FowlerExample.png)

.center[Fowler (1981)]
]

---
.pull.left[
## **Concave curves:** Butterflies
]

.pull-right[When **density dependent effects** kick in when populations are **small** rather than **large**.]

![](images/butterfly.png)
.center[(Nowicki et al. 2009)]

---

## Carrying capacity

.pull-left.large[
**Ecological carrying capacity**

Basically - *K* of a logistic growth

Limited (almost always) by:

- resources: 
  - food
  - shelter
  - breeding **habitat**

- space

- interactions (predation / parasites / disease)
]

.pull-right[
> For the  **Howework assignment** you will explore different ways in which **Ecological Carrying Capacity** is estimated, and why it is an important question for wildlife ecologists to ask. 
]

---

.pull-left-60[
#### ***Kinds of "Carrying Capacity"***

### Ecological carrying capacity

**The natural limit** - **K** in logistic equation

- Set by **resources** in the environment
- Population equilibrium from density-dependence
  - lack of food, space, cover | predators | disease | etc.
- Can change as environment changes

### Economic carrying capacity

**Maximum sustained yield** - for harvest/cropping

- Population level for maximum offtake
- Used by range managers, animal production
- **Well below** ecological K
- For logistic growth: **K/2** or 50% of ecological K

]

.pull-right-40[
![](Lecture_PopulationEcology_PartII_files/figure-html/economicK-1.png)
]

---

#### ***Kinds of "Carrying Capacity"***

.pull-left[

### Social / Cultural carrying capacity

**Human tolerance level** - varies by context

**Examples:**

Wolves on Wyoming ranch: **K = 0**  
-   *(no tolerance for livestock predation)*

Elephants near tourist hotels in Serengeti: 
- **K < ecological K**  to preserve scenic Acacia trees for tourism

Urban deer in residential areas: 
- **highly variable**  *(depends on garden/road collision damage tolerance)*
]

.pull-right[
![](images/serengeti-acacia-camps.jpg)
.center[(Fryxell Chapter 8)]

]

---

## Some references

.small[
- Benton T G, A Grant, and T H Clutton-Brock. 1995. Does environmental stochasticity matter? Analysis of red deer life-histories on Rum. Evolutionary Ecology 9:559–574. [link](https://doi.org/10.1007/BF01237655)
- Caughley G and C J Krebs. 1983. Are Big Mammals Simply Little Mammals Writ Large? Oecologia 59:7-17. [link](https://doi.org/10.1007/BF00388065)
- Chapman E J and C J Byron. 2018. The flexible application of carrying capacity in ecology. Global Ecology and Conservation 13:e00365. [link](https://doi.org/10.1016/j.gecco.2017.e00365)
- Fowler C W. 1981. Density Dependence as Related to Life History Strategy. Ecology 62:602–610. [link](https://doi.org/10.2307/1937727)
- Laidre K L, R J Jameson, S J Jeffries, R C Hobbs, C E Bowlby, and G R VanBlaricom. 2002. Estimates of carrying capacity for sea otters in Washington state. Wildlife Society Bulletin 30:1172–1181. [link](https://www.jstor.org/stable/3784286)
- McClelland C J R, C K Denny, T A Larsen, G B Stenhouse, and S E Nielsen. 2021. Landscape estimates of carrying capacity for grizzly bears using nutritional energy supply for management and conservation planning. Journal for Nature Conservation 62:126018. [link](https://doi.org/10.1016/j.jnc.2021.126018)
- Nowicki P, S Bonelli, F Barbero, and E Balletto. 2009. Relative importance of density-dependent regulation and environmental stochasticity for butterfly population dynamics. Oecologia 161:227–239. [link](https://doi.org/10.1007/s00442-009-1373-2)
- Potvin F and J Huot. 1983. Estimating Carrying Capacity of a White-Tailed Deer Wintering Area in Quebec. The Journal of Wildlife Management 47:463-475. [link](https://www.jstor.org/stable/3808519)
- Sibly R M, D Barker, M C Denham, J Hone, and M Pagel. 2005. On the Regulation of Populations of Mammals, Birds, Fish, and Insects. Science 309:607–610. [link](https://doi.org/10.1126/science.1110760)
- Thébault J, T S Schraga, J E Cloern, and E G Dunlavey. 2008. Primary production and carrying capacity of former salt ponds after reconnection to San Francisco Bay. Wetlands 28:841–851. [link](https://link.springer.com/article/10.1672/07-190.1)
- Wydeven A P, T R Van Deelen, and E J Heske, editors. 2009. Recovery of Gray Wolves in the Great Lakes Region of the United States: An Endangered Species Success Story. Springer New York, New York, NY. [link](https://doi.org/10.1007/978-0-387-85952-1)
]