4  Complex Numbers are Simple

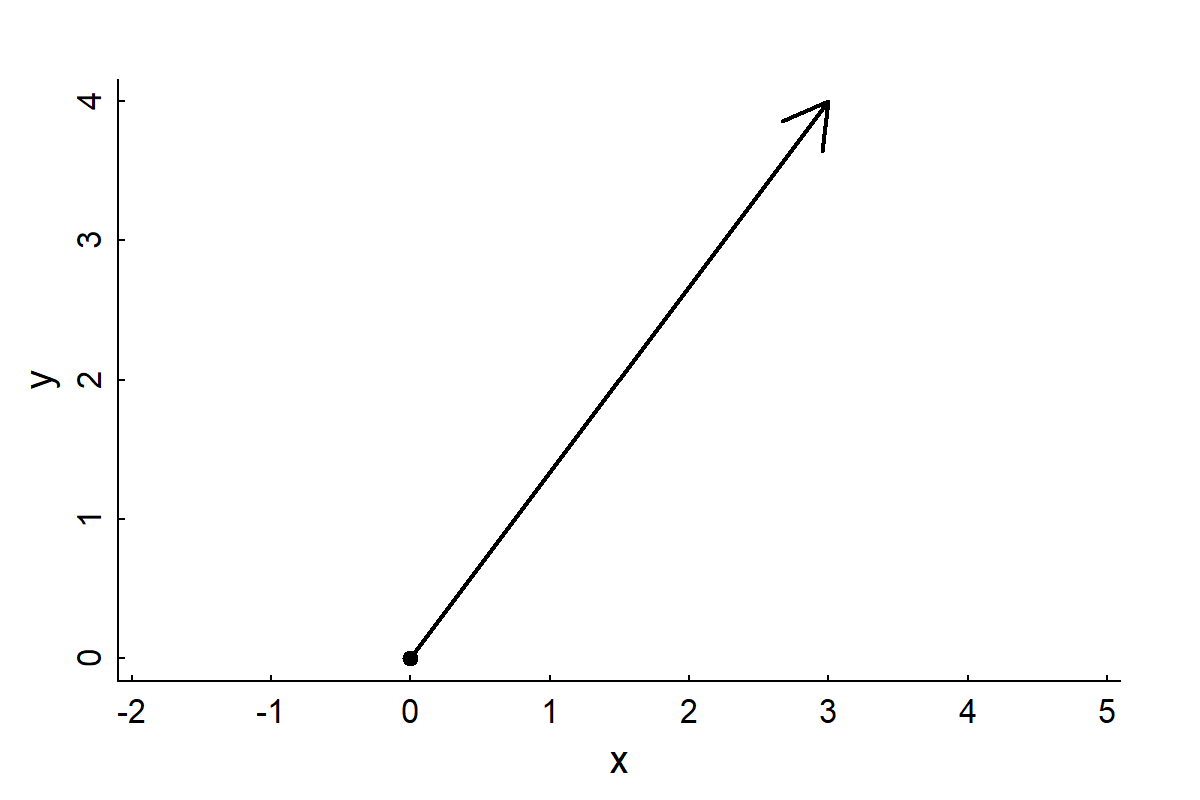
Complex numbers are the single most efficient way to deal with 2D vectors, both in math notation and in R code!

4.1 Why complex numbers? (a teaser)

When studying animal movement data, or, really, any spatial data, we constantly work with two-dimensional coordinates (\(x, y\)). Traditional approaches often treat these coordinates separately, leading to cumbersome calculations.

Just as a very basic example, say you have a location \(\{x,y\}\) in 2D space. So \(x = 3\) and \(y = 4\). We’d like to get very comfortable thinking of pairs of points as vectors. In particular, in this case, as a vector that goes from (0,0) to (3,4). Here’s a picture:

x <- 3; y<- 4
plot(x,y, asp = 1, 
     xlim = c(0,x), ylim = c(0,y), 
     type = "n")
points(0,0, pch = 19)
arrows(0,0,x,y, lwd = 2)

Two simple questions. First - what is the length of the vector? That’s easy. We know the Pythagorean theorem, that the hypotenuse is:

\[||z|| = \sqrt{x^2 + y^2}\]1

1 z here is a vector - it contains a distance and an angle, and that \(||z||\) notation - just means “length of vector z”.

That’s not too difficult. Sometimes it aligns very well:

sqrt(x^2 + y^2)
[1] 5

But what about the angle \(\theta\) of this vector? Well … if all you have is \(X\) and \(Y\), the formula for the angle is completely insane:

\[ \theta(x,y) = \begin{cases} \arctan\left(\frac y x\right) &\text{if } x > 0, \\[5mu] \arctan\left(\frac y x\right) + \pi &\text{if } x < 0 \text{ and } y \ge 0, \\[5mu] \arctan\left(\frac y x\right) - \pi &\text{if } x < 0 \text{ and } y < 0, \\[5mu] +\frac{\pi}{2} &\text{if } x = 0 \text{ and } y > 0, \\[5mu] -\frac{\pi}{2} &\text{if } x = 0 \text{ and } y < 0, \\[5mu] \text{undefined} &\text{if } x = 0 \text{ and } y = 0. \end{cases} \]

What!? It’s complicated because the respective sign of x and y has all kind of impact. There is zero desire to write this out in R.

As a very short summary spoiler: writing \(z\) as a complex number makes this calculation - and many many other extremely useful ones for movement data - instantaneous and trivial.

4.2 Components of complex number

Complex numbers are, essentially, a handy bookkeeping tool to package together two dimensions in a single quantity. They also simultaneously express both Cartesian coordinates (position) and polar coordinates (distance and direction). This dual nature makes them exceptionally well-suited for movement analysis, where we care about both where an animal is and how it’s moving.

They expand the one-dimensional (“Real”) number line into a second dimension (“Imaginary”).

We write a complex number \(Z = X + iY\)

  • \(X\) is the real part.
  • \(Y\) is the imaginary part.
  • \(i\) is the imaginary unit, where \(i^2 = -1\)

The same number can be written in terms of distances and angles, which are the two basic movement metrics of greatest practical interest:

\[ Z = R \, \exp(i \theta) = R(\cos \theta + i \sin \theta) \]

where: - \(R\) is the length of the vector from the origin, aka modulus or magnitude - \(\theta\) is the orientation of the vector, aka the argument

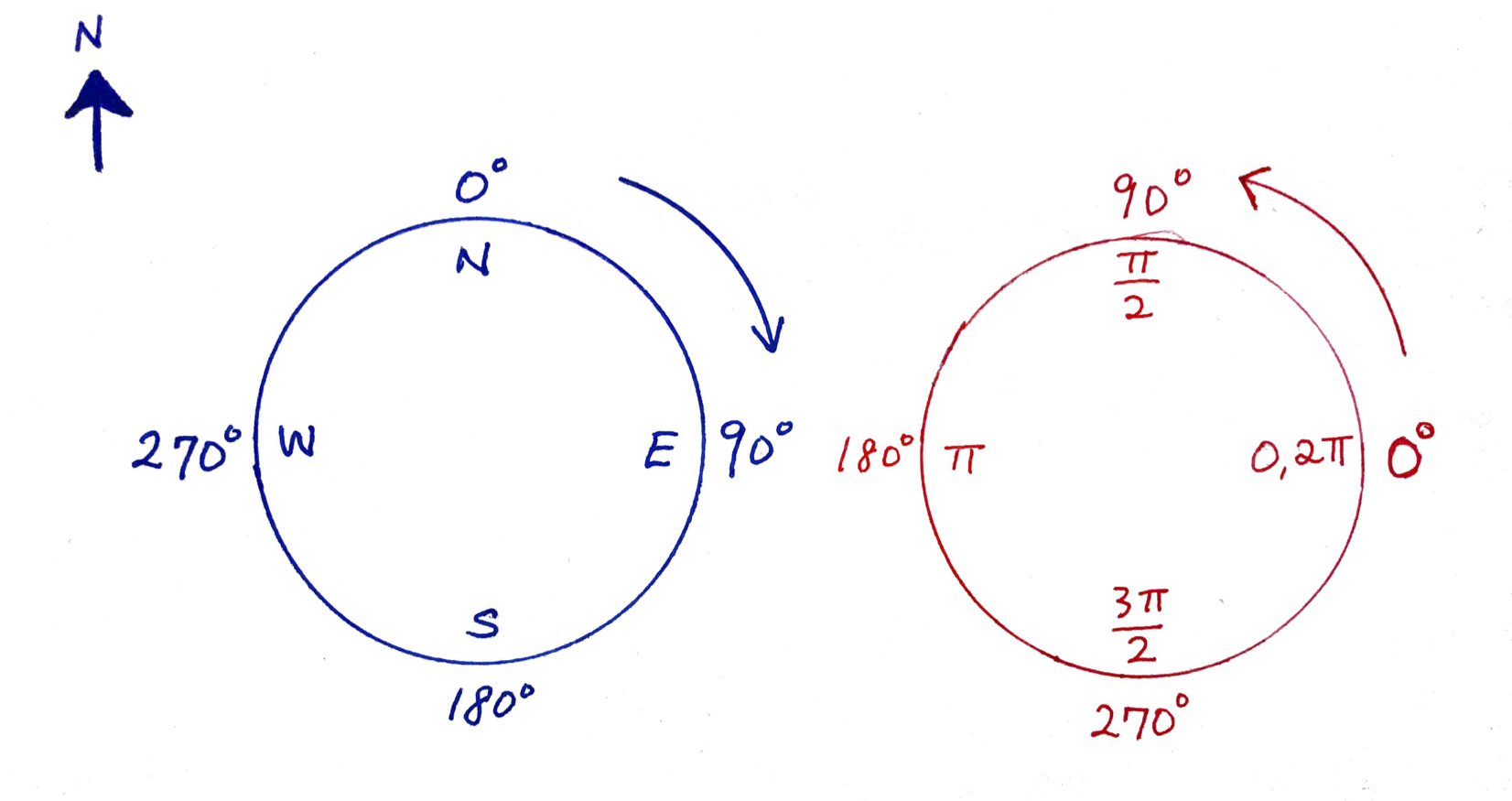
This angle, \(\theta\) is defined in radians that turn counter-clockwise from the x-axis, \(\pi/2\) is on the y-axis, \(\pi\) is on the negative x-axis, etc. You can see that by simply putting in some numbers:

\[Z = 1 = \exp{0}\] \[Z = 0 + 1i = \exp{(i \pi/2)}\]

All of these have modulus 1.

Learning to count angles counter-clockwise from the East, rather than clockwise from North. And by \(\pi\), not 180\(^o\).

4.2.1 In R

X <- c(3,4,-2)
Y <- c(0,3,2)
Z <- X + 1i*Y
Z
[1]  3+0i  4+3i -2+2i

Alternatively:

Z <- complex(re = X, im=Y)
plot(Z, pch=19, col=1:3, asp=1)
arrows(rep(0,length(Z)), rep(0,length(Z)), Re(Z), Im(Z), lwd=2, col=1:3)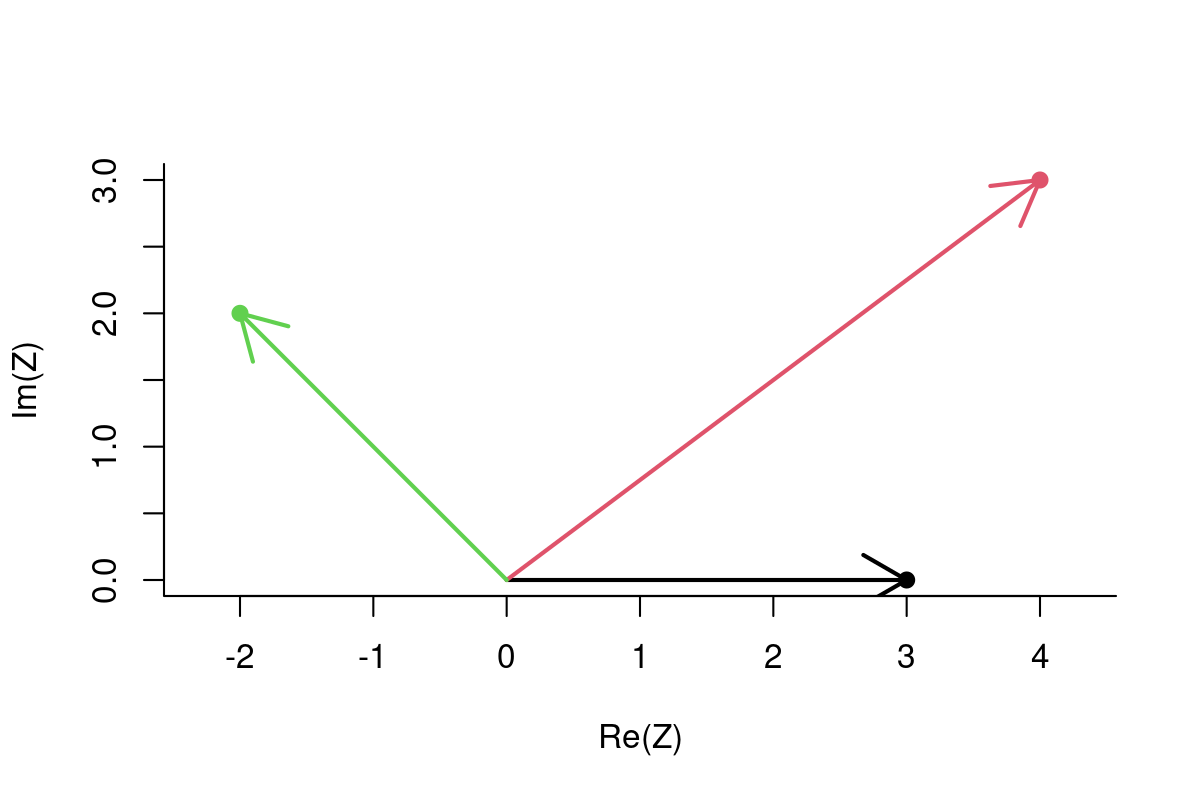

Note: ALWAYS use asp=1 - “aspect ratio = 1:1” - when plotting (properly projected) movement data!

Obtaining summary statistics is nearly instant. Obtain lengths of vectors:

Mod(Z)
[1] 3.000000 5.000000 2.828427

Obtain orientation of vectors:

Arg(Z)
[1] 0.0000000 0.6435011 2.3561945

Note, the orientations are in radians, i.e. range from \(0\) to \(2\pi\) going counter-clockwise from the \(x\)-axis. Compass directions go from 0 to 360 clockwise, so, to convert:

90-(Arg(Z)*180)/pi
[1]  90.0000  53.1301 -45.0000

4.3 Quickly simulating a path

Quick code for a correlated random walk:

X <- cumsum(arima.sim(n=100, model=list(ar=.7)))
Y <- cumsum(arima.sim(n=100, model=list(ar=.7)))
Z <- X + 1i*Y
plot(Z, type="o", asp=1)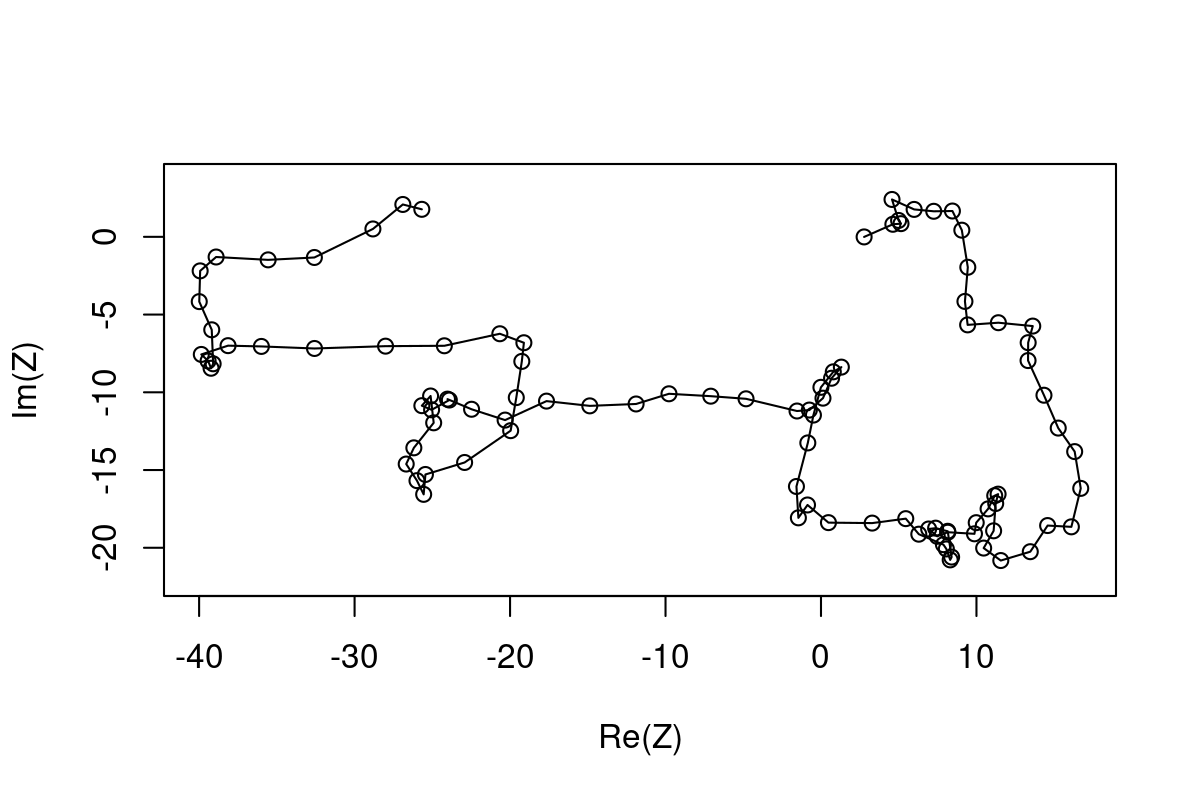

Instant summary statistics of a trajectory:

The average location

mean(Z)
[1] -23.95766+24.39845i

The step vectors:

dZ <- diff(Z)
plot(dZ, asp=1, type="n")
arrows(rep(0, length(dZ)), rep(0, length(dZ)), Re(dZ), Im(dZ), col=rgb(0,0,0,.5), lwd=2, length=0.1)

Distribution of step lengths:

S <- Mod(dZ)
summary(S)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.1718  1.1010  1.8296  1.9793  2.6824  5.6392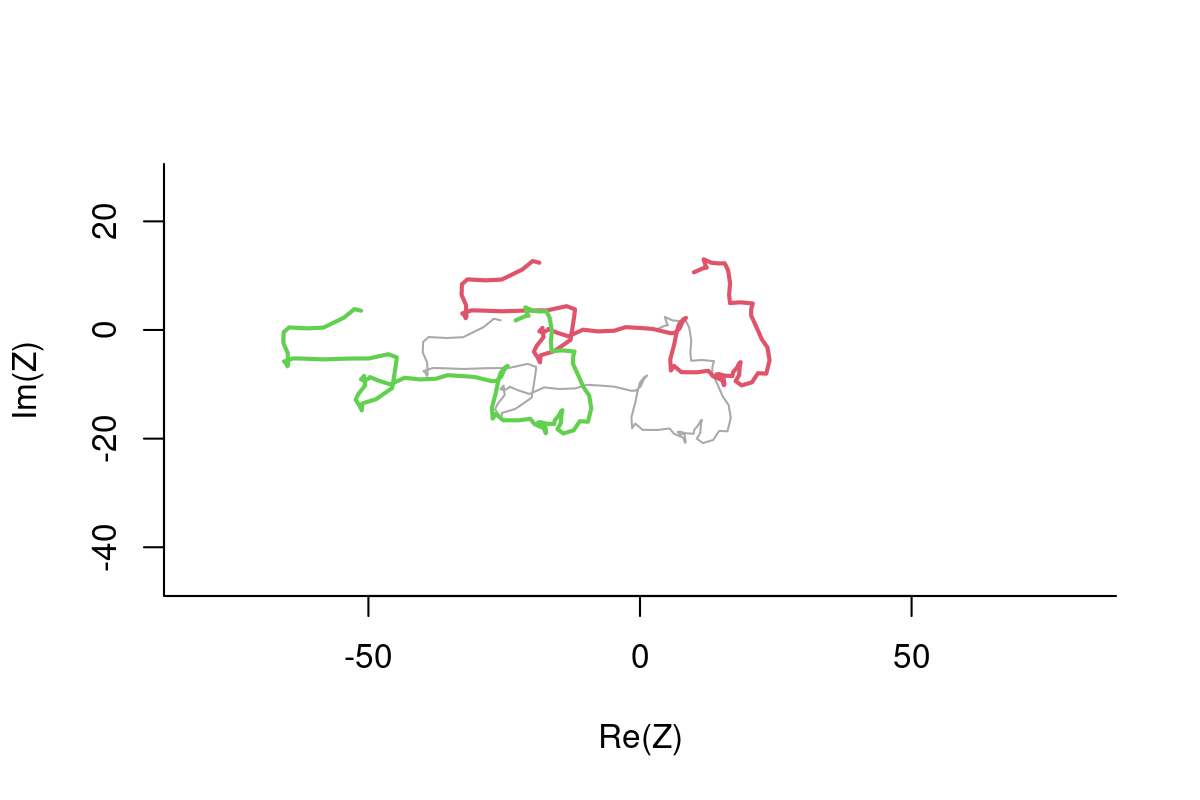 
hist(S, col="grey", bor="darkgrey", freq=FALSE)
lines(density(S), col=2, lwd=2)

What about angles?

  • The absolute orientations:
Phi <- Arg(dZ)
hist(Phi, col="grey", bor="darkgrey", freq=FALSE, breaks=seq(-pi,pi,pi/3))

  • Turning angles
Theta <- diff(Phi)
hist(Theta, col="grey", bor="darkgrey", freq=FALSE)

QUESTION: What is a problem with this histogram?

Circular statistics:

Angles are a wrapped continuous variable, i.e. \(180^o > 0^o = 360^o < 180^o\). The best way to visualize the distribution of wrapped variables is with Rose-Diagrams. An R package that deals with circular data is circular.

require(circular)
Theta <- as.circular(Theta)
Phi <- as.circular(Phi)
rose.diag(Phi, bins=16, col="grey", prop=2, main=expression(Phi))
rose.diag(Theta, bins=16, col="grey", prop=2, main=expression(Theta))

LAB EXERCISE

  1. Load movement data of choice!
  2. Convert the locations to a complex variable Z.
  3. Obtain a vector of time stamps T, draw a histogram of the time intervals. Then, ignore those differences.
  4. Obtain, summarize and illustrate:
  • the step lengths
  • the absolute orientation
  • the turning angles

4.4 Complex manipulations (are easy)

4.4.1 Addition & substration of vectors

Addition and subtraction of vectors:

\[ Z_1 = X_1 + i Y_1; Z_2 = X_2 + i Y_2\] \[ Z_1 + Z_2 = (X_1 + X_2) + i(Y_1 + Y_2)\]

Useful, e.g., for shifting locations:

plot(Z, asp=1, type="l", col="darkgrey", xlim=c(-2,2)*max(Mod(Z)))
lines(Z - mean(Z), col=2, lwd=2)
lines(Z + Z[length(Z)], col=3, lwd=2)

4.4.2 Rotation of vectors

Multiplication of complex vectors \[Z_1 = R_1 \exp(i \theta_1); Z_2 = R_2 \exp(i \theta_2)\] \[ Z_1 Z_2 = R_1 R_2 \exp(i (\theta_1 + \theta_2))\] Note the magic of the rotation summing! If \(\text{Mod}(Z_2) = 1\), multiplications rotates by \(\text{Arg}(Z_2)\)

theta1 <- complex(mod=1, arg=pi/4)
theta2 <- complex(mod=1, arg=-pi/4)

plot(Z, asp=1, type="l", col="darkgrey", lwd=3)
lines(Z*theta1, col=2, lwd=2)
lines(Z*theta2, col=3, lwd=2)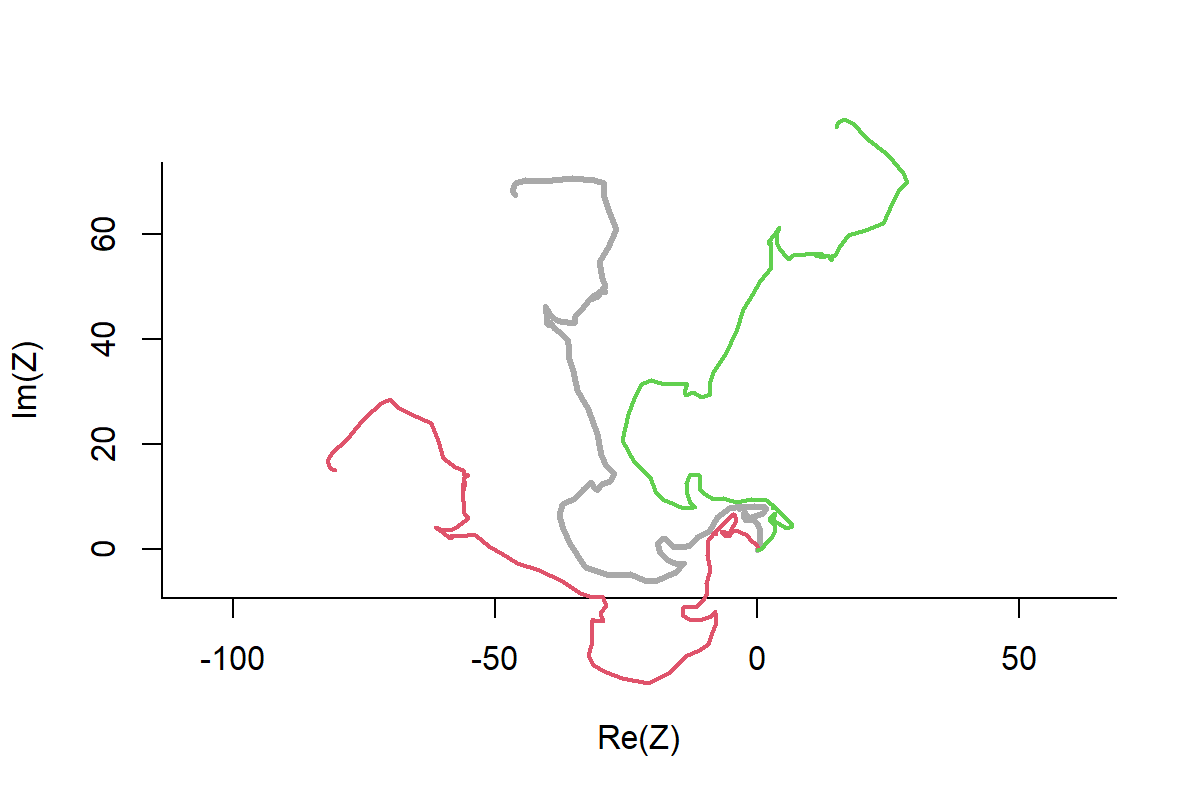

A colorful loop:

require(gplots)
plot(Z, asp=1, type="n", xlim=c(-1,1)*max(Mod(Z)), ylim=c(-1,1)*max(Mod(Z)))
cols <- rich.colors(1000,alpha=0.1)
thetas <- seq(0,2*pi,length=100)
for(i in 1:1000)
  lines(Z*complex(mod=1, arg=thetas[i]), col=cols[i], lwd=4)

I know you’re probably thinking …

“Thanks for teaching me how to make a weird swirling rainbow thing … but why in the world would I want to shift and rotate my precious, precious data, which was just perfect the way it was?

My response: Null Sets for Pseudo Absences!

4.5 Example with Finnish Wolves

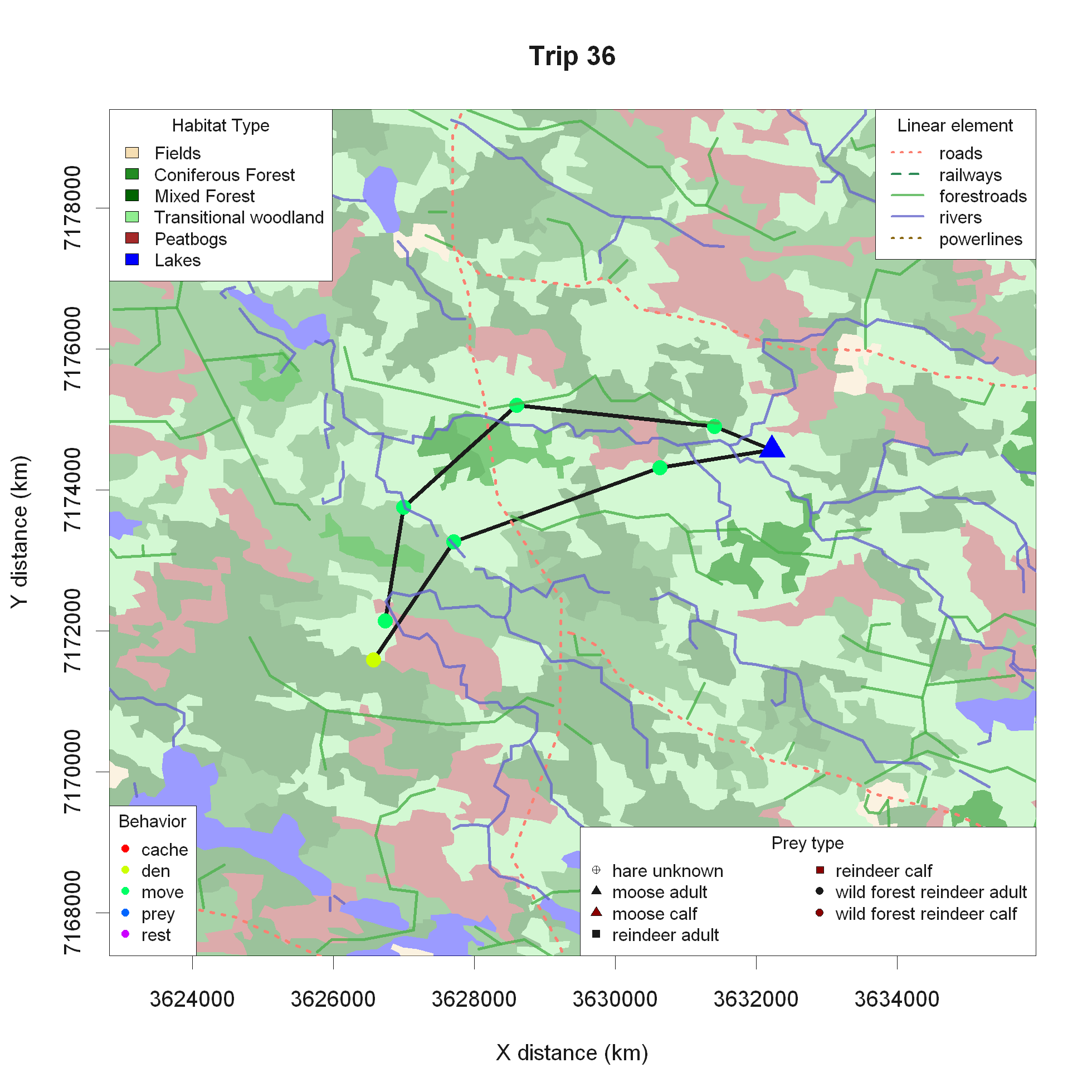
In-depth summer predation study, questions related to habitat use, landscape type - forest/bog/field - linear elements - roads/rivers/power lines, etc.

4.5.1 Defining Null Sets

  1. Obtain all the steps and turning angles
  2. Rotate them by the orientation of the last step (\(Arg(Z_1-Z_0)\))
  3. Add the rotated steps to the last step (\(Z_1\))

Null step illustration
  1. Obtain all the steps and turning angles
  2. Rotate them by the orientation of the last step (\(Arg(Z_1-Z_0)\))
n <- length(Z)
S <- Mod(diff(Z))
Phi <- Arg(diff(Z))
Theta <- diff(Phi)
RelSteps <- complex(mod = S[-1], arg=Theta)

Z0 <- Z[-((n-1):n)]
Z1 <- Z[-c(1,n)]
Z2 <- Z[-(1:2)]

Rotate <- complex(mod = 1, arg=Arg(Z1-Z0))
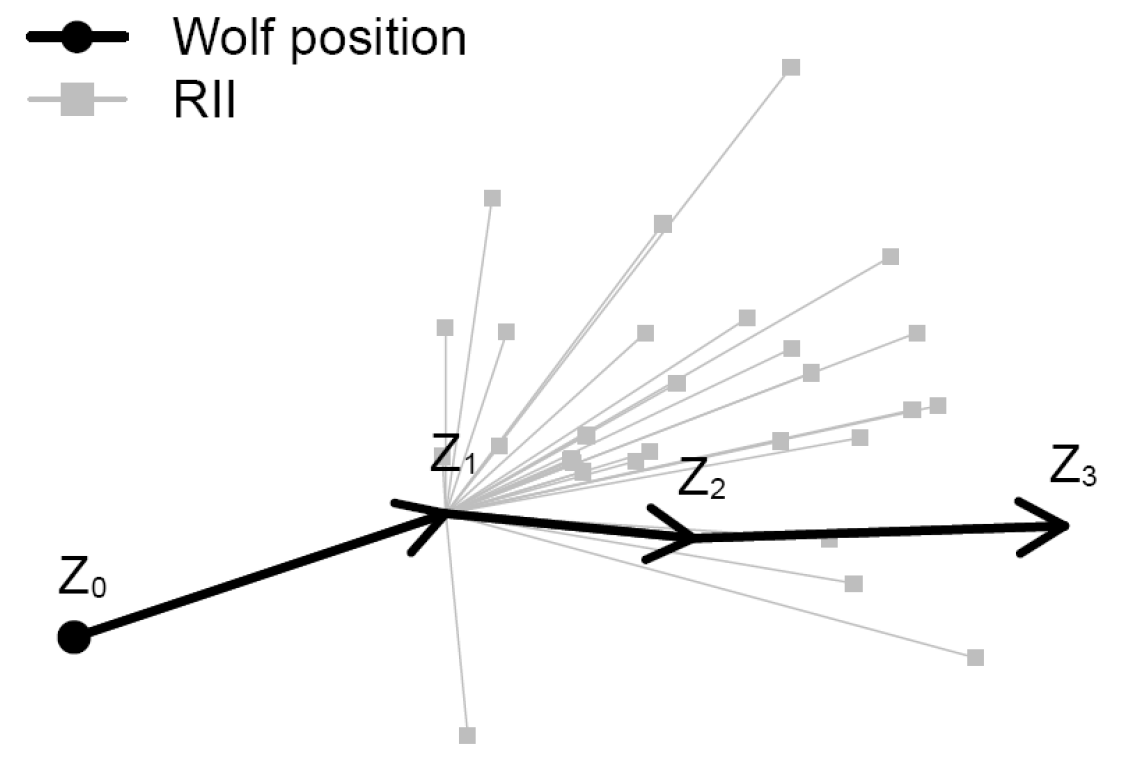
plot(c(0, RelSteps), asp=1, xlab="x", ylab="y", pch=19)
arrows(rep(0,n-2), rep(0, n-2), Re(RelSteps), Im(RelSteps), col="darkgrey")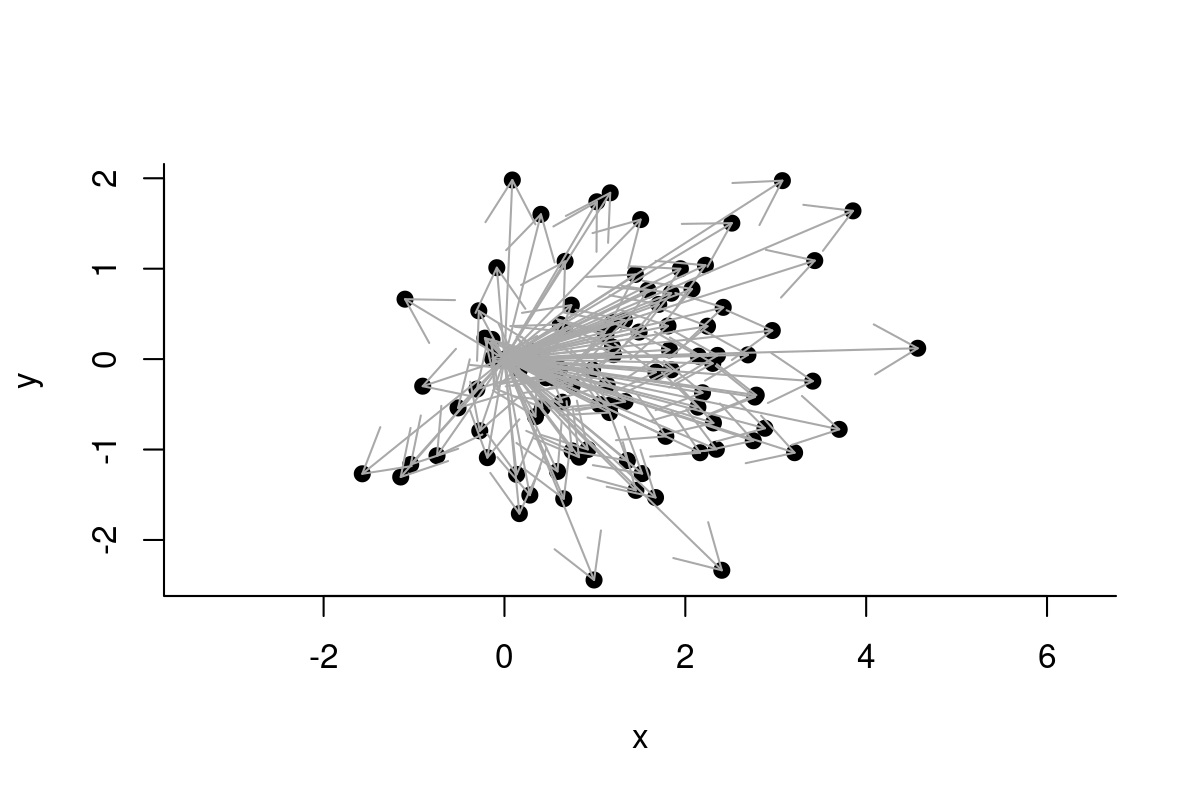

Note: in practice (i.e. with tons of data), it is sufficient to randomly sample some smaller number (e.g. 30) null steps at each location.

  1. Add the rotated steps to the last step
Z.null <- matrix(0, ncol=n-2, nrow=n-2)
for(i in 1:length(Z1))
  Z.null[i,] <- Z1[i] + RelSteps * Rotate[i]
  1. Make the fuzzy catterpillar plot
plot(Z, type="o", col=1:length(Z), pch=19, asp=1)
for(i in 1:nrow(Z.null))
  segments(rep(Re(Z1[i]), n-2), rep(Im(Z1[i]), n-2), 
           Re(Z.null[i,]), Im(Z.null[i,]), col=i+1)

4.5.2 Null set

The use of the null set is a way to test a narrower null hypothesis that accounts for auto correlation in the data.

The places the animal COULD HAVE but DID NOT go to are pseudo-absences, against which you can fit, e.g., logistic regression models (aka Step-selection functions).

Or just be simple/lazy (like us) and compare observed locations with Chi-squared tests:

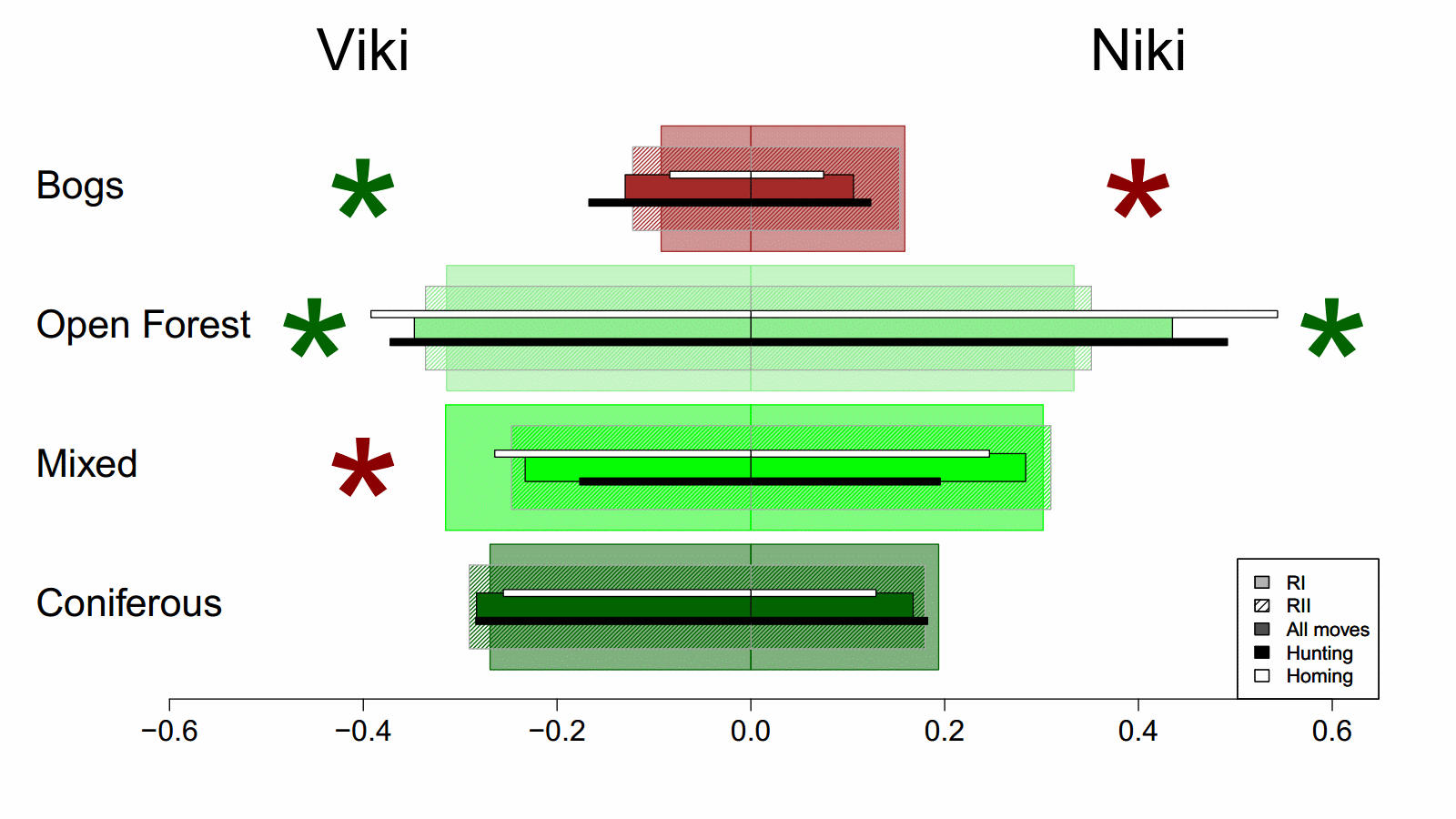
EXERCISE: Create a fuzzy-catterpillar plot!

Use (a portion) of the data you analyzed before.

# get pieces
n <- length(Z)
Steps <- diff(Z)
S <- Mod(Steps)
Phi <- Arg(Steps)
Theta <- diff(Phi)
RelSteps <- complex(mod = S[-1], arg = Theta)

# calculate null set
Z0 <- Z[1:(n-2)]
Z1 <- Z[2:(n-1)]
Z2 <- Z[3:n]
Rotate <- complex(mod = 1, arg = Arg(Z1-Z0))

Z.null <- matrix(NA, ncol=n-2, nrow=n-2)
for(i in 1:length(Z1))
  Z.null[i,] <- Z1[i] + sample(RelSteps) * Rotate[i]

# plot
plot(Z, type="o", col=1:10, pch=19, asp=1)
for(i in 1:nrow(Z.null))
  segments(rep(Re(Z1[i]), n-2), rep(Im(Z1[i]), n-2), 
           Re(Z.null[i,]), Im(Z.null[i,]), col=i+1)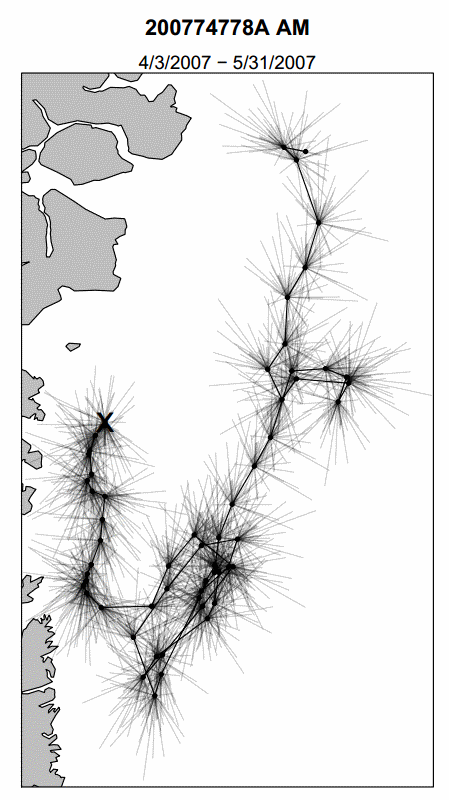

Fuzzy Polar Bear Catterpillar!

4.6 Conclusion

Complex numbers provide a powerful, elegant framework for movement analysis that:

  • Simplifies calculations: No need to separately track x and y coordinates
  • Preserves spatial relationships: Distances and angles are automatically maintained
  • Enables vectorized operations: R can process entire paths at once
  • Facilitates advanced analysis: Easy computation of turning angles, path metrics
  • Scales efficiently: Works equally well for short tracks or massive datasets

Complex numbers teach us to think in terms of vectors, and allow us to transform cumbersome spatial calculations into intuitive vector operations, making movement analysis accessible and efficient.